SONNETS MATH (INTRO)
The BARDCODE video reveals several layers of discoveries.
Discovery 1: By connecting four punctuation dots and two horizontal line endings in the 1609 Sonnets title page, four perfect right-angled triangles are revealed, one being the iconic 3:4:5 Pythagorean triangle.
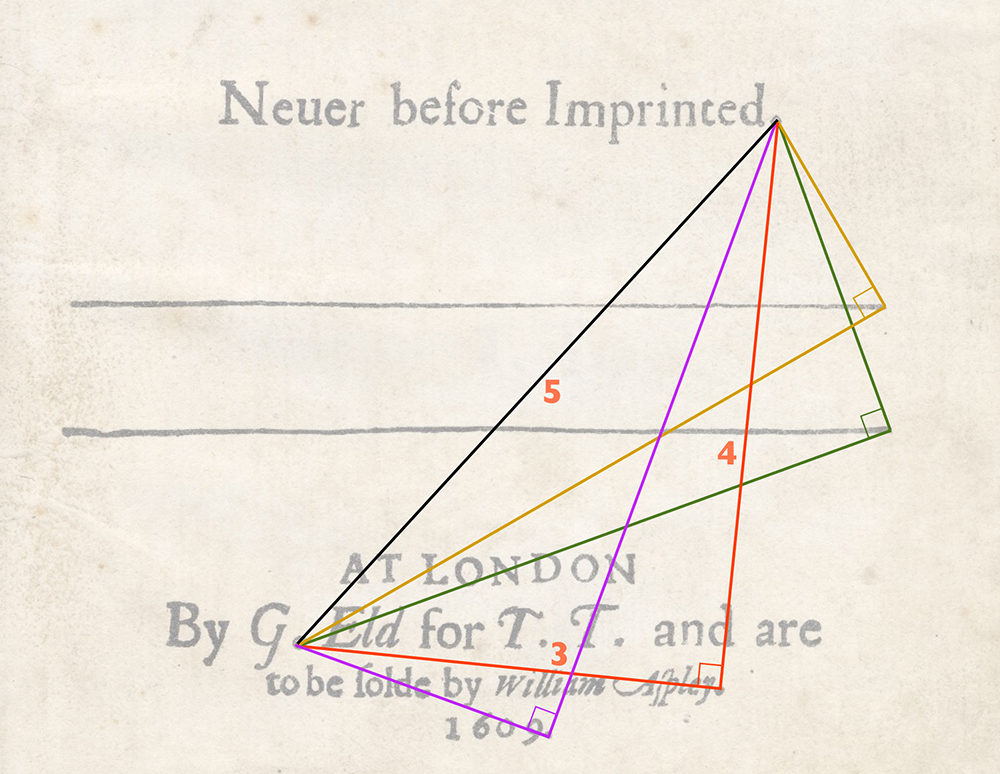
Several YouTube commentators have claimed it’s quite normal to find perfect right-angled triangles resulting from a few random dots. Apparently this is a common misconception so we must examine it briefly.
The probability of a right-angled triangle resulting from three dots placed at random approaches nil as the dot sizes approach zero-width — technically a Euclidean ‘point’. But allowing for dots to have ‘size’ and stipulating that a line vertex can fall anywhere within the area bounded by the dot, we can calculate probability as a specific factor of the dot area to page area ratio.
Taking just the reduced area of the Sonnets page shown above and comparing it to the size of the 1609 dot, a conservative estimate for the probability of a right triangle occurring completely by chance is 60 to 1. That doesn’t seem like much but the probability decreases exponentially as the number of triangles increases. Since the Sonnets page has four triangles the answer is 60 x 60 x 60 x 60 to 1. In other words, there’s about one chance in 13 million of this design being random.*
But that’s only the first step. It postulates the four triangles showing up anywhere on the page using 12 randomly chosen points. The Sonnets designer, however, used the absolute minimum possible (6 points) to create four right triangles sharing a common hypotenuse. The probability obviously reduces as the points decrease from 12 to 6 so we could work out an algorithm and come up with a number… 13 million times ‘#’, perhaps? But why bother?
That would be only the second step. Next, we’d have to figure out the odds of one of the four being not just any right triangle but the iconic Pythagorean 3:4:5 triangle! (13 million times ‘#’ times ‘x’ ?) Finally, we’d need to confront the most baffling conundrum of all: what are the odds of one of the triangles having line lengths whose ratio reveals π? Or e? Or ø? To three decimals? Whatever that number is, exponentiate it to the power of 12 (for 12 constants) then multiply by 13 million times ‘#’ times ‘x’. Call your doctor if symptoms of doubt persist.
*Initial estimate by Daniel P. Hurley, PhD., professor of Computer Science and Information Systems at Santa Monica College, California.
Discovery 2: A perfect circle can be made to pass through all six points. Where the circle’s circumference passes through the two horizontal lines another two right-angled triangles are formed.
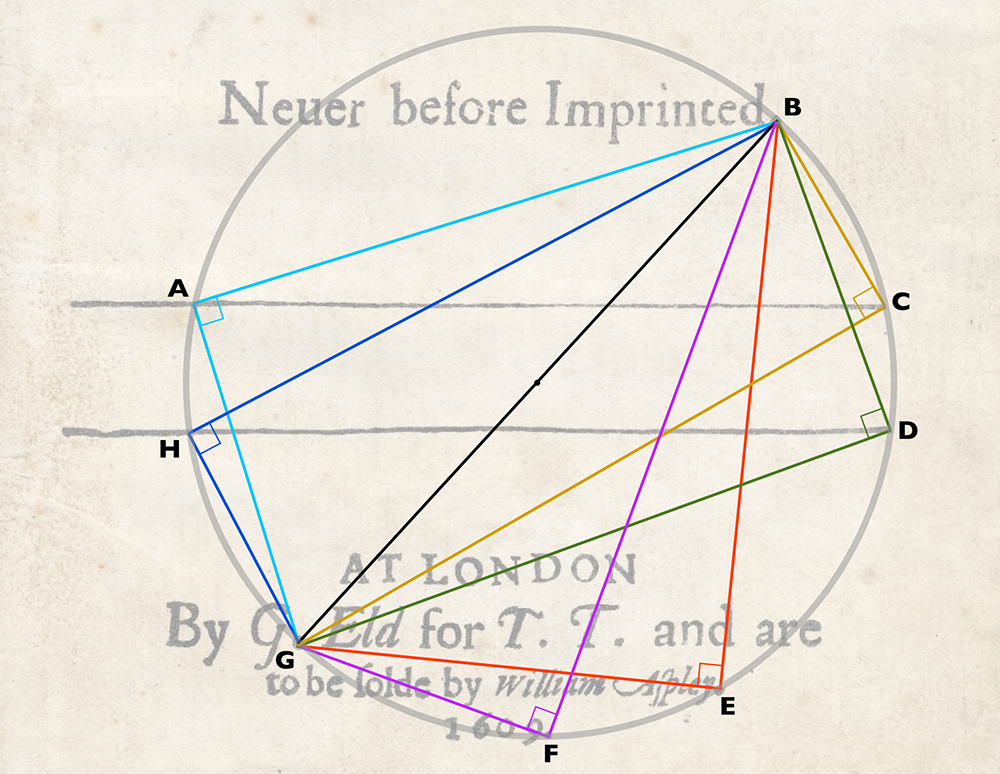
At this stage it should be obvious we’re witnessing more than just an exercise in creating right triangles. This is a visual representation of Thales Theorem — in itself a huge clue. Thales was the first person to measure the height of the Great Pyramid and he did it using the geometry of right-angled triangles.
Discovery 3: Rough, ballpark measuring of the line segments, followed by calculating the ratios of the smaller sides of each triangle, reveals values very close to several significant math constants. But close results, in and of themselves, are not accurate enough to prove intentionality.
Methodology
This is as far as most curious observers have gone. Hobbled by the imprecision of rough or incomplete methods they’ve deemed the BARDCODE results inaccurate. But abandoning such initial estimates because they’re only close is missing the big picture. The astronomical odds against randomness clearly indicate these dots and lines were placed with painstaking exactitude so we owe it to the creator of this masterpiece to measure everything with the greatest rigour possible.
For such an exacting task I used the world’s highest resolution digital copy of the original Sonnets title page, licensed from the Folger Shakespeare Library in Washington, D.C.. I then blew it up to 5x magnification in order to assure the highest accuracy possible.
You could do the same if you want to invest that much time and money. Unfortunately the copyright of that image is owned by the Folger so I cannot replicate it directly online without incurring escalating expenses as more and more people become interested in these discoveries. So what you see in the YouTube videos and these pdf files is a lower resolution alternate source copy. Nevertheless, it’s been checked thoroughly against the high resolution file and conveys a faithful facsimile, accurate enough to allay doubts about the three decimal precision of the calculations.
For those who still want to actually reproduce these findings themselves please write to me (alan@ToBeOrNotToBe.org) with proof that you’ve licenced the Folger hi-res digital file and I’ll gladly assist your efforts by sending you my actual work files. To access and edit them you’ll need Apple’s Keynote 10.0 or higher and a recent Mac. (I believe Windows can now run Keynote but I can’t vouch for its accuracy.)
How to prove this yourself
Each line was precisely drawn and measured using Keynote 7.2 originally (accurate to 2 decimal places measuring lengths and to 1 decimal place measuring angles). We’re interested in ratios so the actual system of measures is irrelevant. But for reference the dimensions seen printed on each diagram are in centimeters as measured automatically by the software. (When measurements are divided into each other to calculate ratios the results, of course, expand to 5 decimal places and more).
The genius behind the masterpiece
It’s my contention that Dr. John Dee (1527~1608/9) was the brilliant polymath behind the geometric design of this amazing work. (For a thorough documentation of the evidence supporting this claim see Book I, Dee-Coding Shakespeare.
As the foremost mathematician and cryptographer of the age, he knew it is geometrically impossible to connect more than three of these values perfectly to a 3:4:5 triangle sharing a common hypotenuse. If that were the case this hidden connectivity between twelve of the world’s most significant constants would have been discovered long ago. Even a little consideration of this fact should help us realize that far from illustrating ‘fuzzy’ math, Dee’s accomplishment matches what we should expect from the genius who, in 1570, introduced the first full translation of Euclid’s Elements from Latin into English. It’s all the more amazing for the absolute precision and ingenuity of his solution.
In order to connect all twelve constants there inevitably must be very specific, tiny differences in hypotenuse lengths and angles. And there’s only one way to accomplish such a feat. One has to increase the sizes of the G and Imprinted dots on which the end-points of said hypotenuses must land. This is, in fact, the smoking gun that reveals Dee’s methodology because upon close examination we see that he has increased those dots by exactly the amount needed to accommodate those small differences. No more. No less.
Rules of the game
Before we begin, certain ground-rules by which we can judge the placement of a line vertex to be valid or not, must be decided upon. I think most reasonable observers would agree that the following guidelines make the most sense:
1) The vertices of each line must always fall within the boundary of the individual dot they’re landing on. (That would be the only sensible explanation for increasing the hypotenuse dot sizes in the first place… to give Dee some latitude within which to work.)
2) The vertices of each line must also fall on the actual circumference line of the circle. (Otherwise what is the purpose of the circle?)
3) The width of the line that forms the circumference of the circle cannot be the same width as the larger dots; the extra space by which it exceeds the smaller dots would be superfluous. It makes sense therefore that the circumference width should be approximately the average diameter of the smallest dots.
4) The right angle of each triangle must be exact (within the 0.1º limitations of Keynote). Even the software’s tiny imprecision can be overcome by making sure the Pythagorean Theorem (a2 + b2 = c2 ) holds for each triangle.
When these rules are observed the true purpose of the enlarged dots is inherently realized.
In the following 5x magnifications we see the relevant portions of the 3:4:5 triangle, BEG, and triangle BHG (which gives the value of e). Note how both their hypotenuses land precisely at the outer edges of the oversized G and Imprinted dots yet still maintain their place on the circle’s circumference.
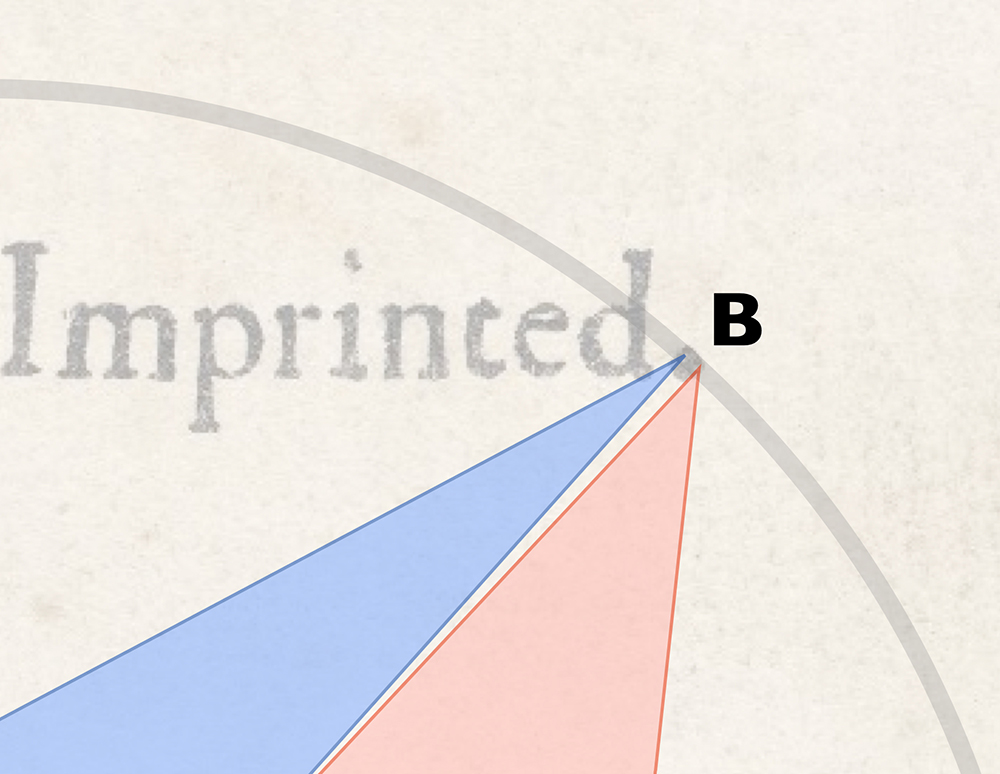

Similarly, the hypotenuses of all six triangles fall somewhere between these two extremes but always within the boundaries of their respective dots and on the circle’s circumference.
In the following diagram (close to original size) we see how this would affect the look of the document if the line segments and circle were actually visible. It’s a very tiny shift but the 3:4:5 triangle is seen to be tilted slightly clockwise.
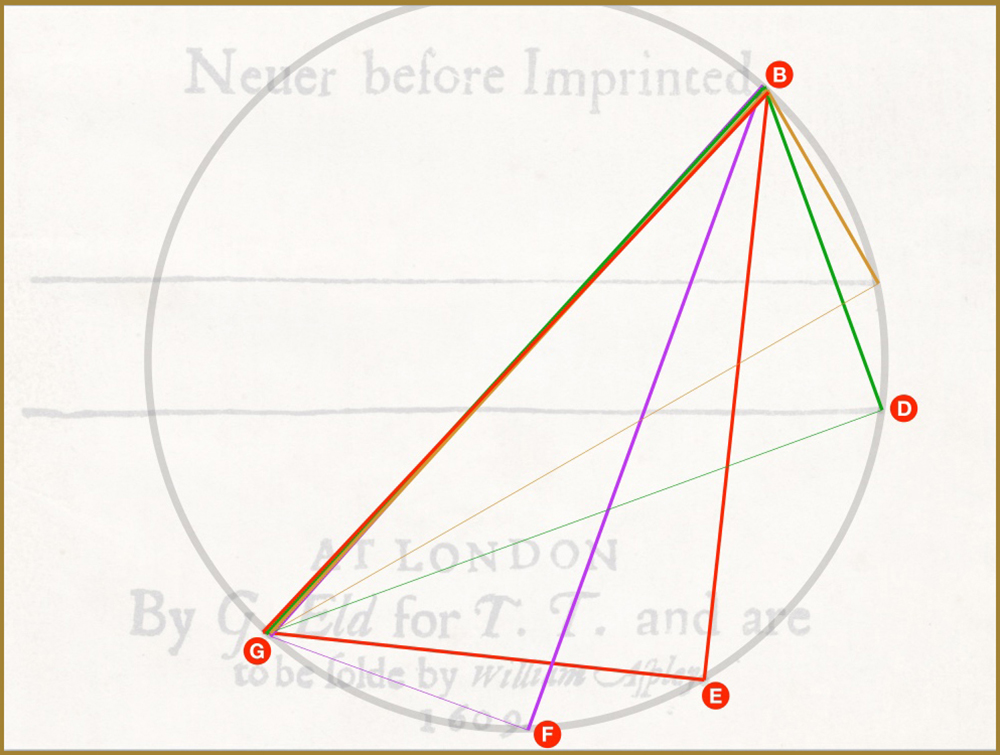
Obviously the only way to have it co-exist with its cousin triangles is to enlarge the G and Imprinted dots (G and B). The fact that they’ve been increased not randomly but (as seen in the two enlarged images above, by the precise amount neccesary to accomodate this geometric mastery) is a clear indication of intentionality.
Having covered the background basics we’re now properly prepared to examine the mathematical data in far greater detail. First I’ll give just the broad strokes so we can begin to grasp the scope of the interconnectedness of everything Dee has created. After that I’ll give the precise numbers for everything including many aspects not shown in the BARDCODE video.
Click here to continue to Sonnets Math (Main).
