
Math ConstantS
Connecting 12 constants on the 4" Sonnets cover to the same 12 constants on the world's largest monument.
It wasn’t until 1836 that Colonel Howard Vyse published the first serious measurements which, given the limited technology available to him, were actually extraordinarily accurate.
They attracted the attention of the publisher of London Magazine, John Taylor, an avid student of mathematics and religion, who was the first to notice close correlations between the pyramid’s basic proportions and the constants Pi and Phi. In 1859 he published The Great Pyramid; Why Was it Built: and Who Built it?, in which he came to the radical conclusion that it was constructed not by the Egyptians but by the Jews. He even went so far as to suggest it was built under the guidance of Moses himself!
The book ignited a furious debate over a subject that came to be known as pyramidology (and whose adherents could all too conveniently be dismissed by academics as pyramidiots). Though Taylor’s biblical assertions were reckless and unprovable, his mathematical insights were nevertheless sound and have persisted as part of the non-traditional conversation ever since.
The following diagrams illustrate the two possibilities that captured Taylor’s imagination. Taking Vyse’s ± uncertainty range into consideration, either of these scenarios could have been the original ratios of the pyramid at the time of its construction.
(NOTE: it’s customary to assign ‘unit value’, 1.0, to the half base or apothem. It doesn’t matter if it’s 1 centimeter or 1 mile; ultimately we’re concerned at this stage with ratio, not the units of measure used.)
The first shows pi ratios. The height xz is in proportion 4/π to the unit apothem. Such a pi-based pyramid would have a side slope angle of 51.854º.
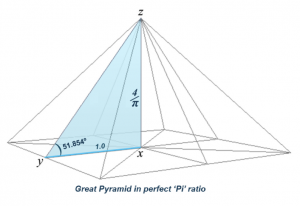
The second shows phi ratios in proportion to the unit apothem. Note that phi appears twice: in the side slope yz as ø, and in the height xz as √ø. Such a phi-based pyramid would have a side slope angle of 51.827º.
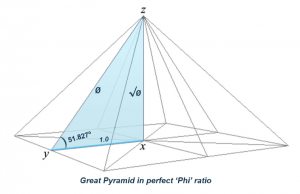
These two angles are so minutely different from each other as to be indistinguishable to the naked eye. Many Egyptologists have undertaken the daunting task of measuring this angle to exacting standards. Here are the five most famous and accurate surveys:

As we can see the average is about midway between the Pi and Phi examples cited above. Just taking the basic assumed original cubit proportions (see below) the angle would be 51.843º. Most orthodox scholars explain this away by saying the ancients hadn’t even invented the wheel yet so how could they possibly know π or ø? It’s pure coincidence! Today’s students of pyramidology however are well grounded in scientific methods, and though their beliefs and approaches may vary, their overarching questions are basically the same:
— Does the pyramid exhibit geometric proportions that suggest a deliberate use of higher mathematics far beyond what could be expected of the early Egyptians? (Or of chance)?
— If so, might there be a more realistic timeline that satisfies all the perceived data?
Up until now it’s been easy for Egyptologists to dismiss a couple of results that show correspondences with just two constants because statistically there’s nothing definitive about such a small sampling. But this is another reason why the Shakespeare Sonnets phenomenon is so significant. We’re confronted with a cryptographic masterpiece that reveals not just the basics, Pi and Phi, but twelve of the most important constants hidden in simple line ratios. Along with these are numerous poetic/mathematical clues, not to mention the precise geographic coordinates of the pyramid itself. The big questions all this provokes are obvious:
— Are the same twelve constants we found in the title page also present in the simple line ratios of Khufu?
If so that would be a far more formidable data set, impossible to explain away as coincidence.
— Is this why the poet has led us to Khufu… to discover the exact same constants?
If so there might possibly be something profound in their relationship that the world can benefit from. Paradigm shifts in both Egyptological and Shakespeare studies would inevitably follow.
Assessing the original dimensions, ratios and specific side slope angle of the Great Pyramid is naturally fraught with difficulty. The monument has suffered at least 4,500 years-worth of damage from weather, natural catastrophes, sand erosion, and so on. Almost the entire outer casing of polished white limestone was looted centuries ago to build mosques and other edifices in and around Cairo. What we see today is the inner core structure of limestone and granite.
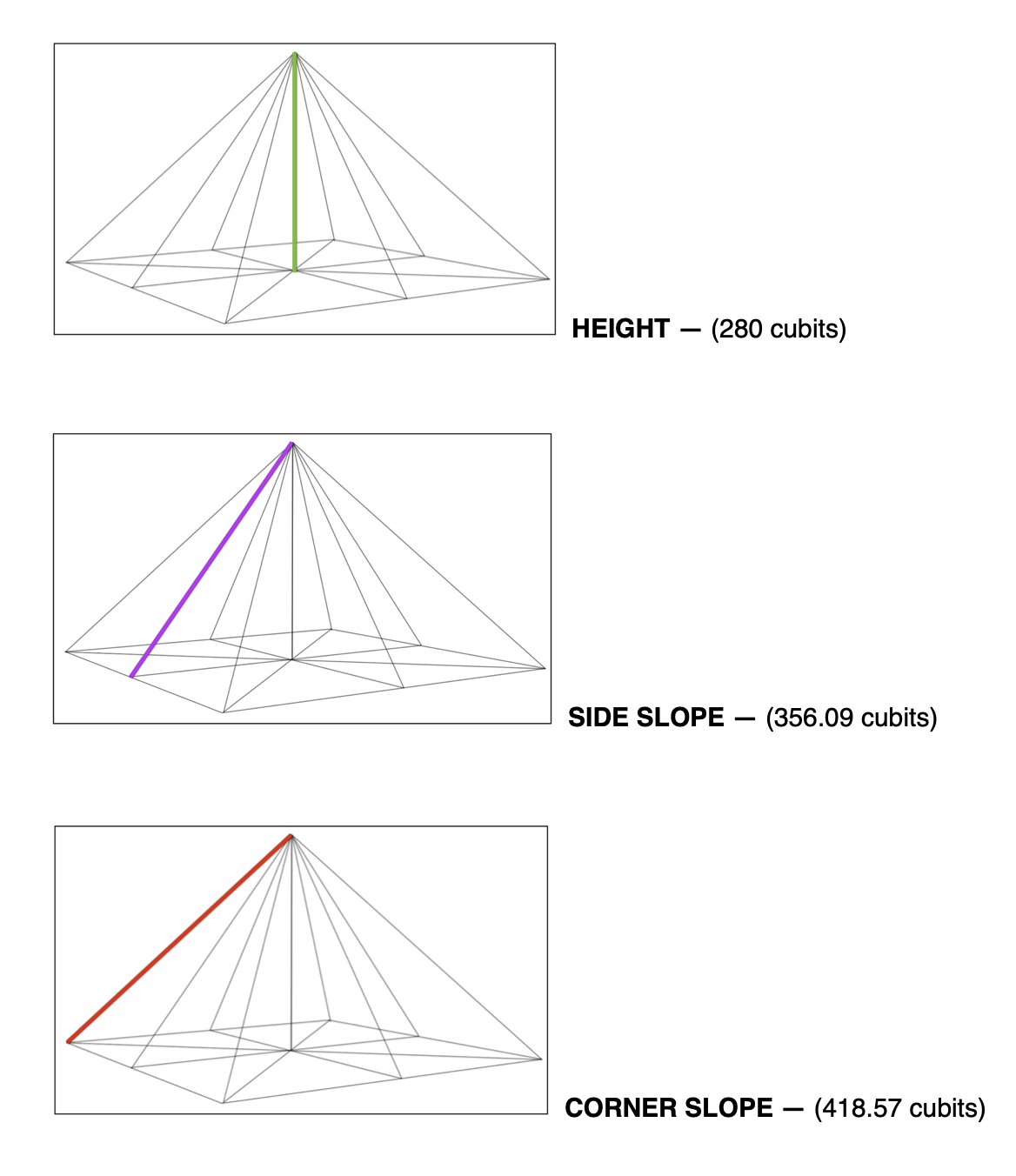
Nevertheless, thanks to conscientious archaeological studies combined with modern technology and computer modeling, scientists are confident they’ve been able to calculate the original dimensions, in royal cubits, to a remarkable level of accuracy. Here then are the six significant proportions that define the pyramid, along with their closest possible original dimensions from which we’ll be able to calculate the ratios we’re interested in.
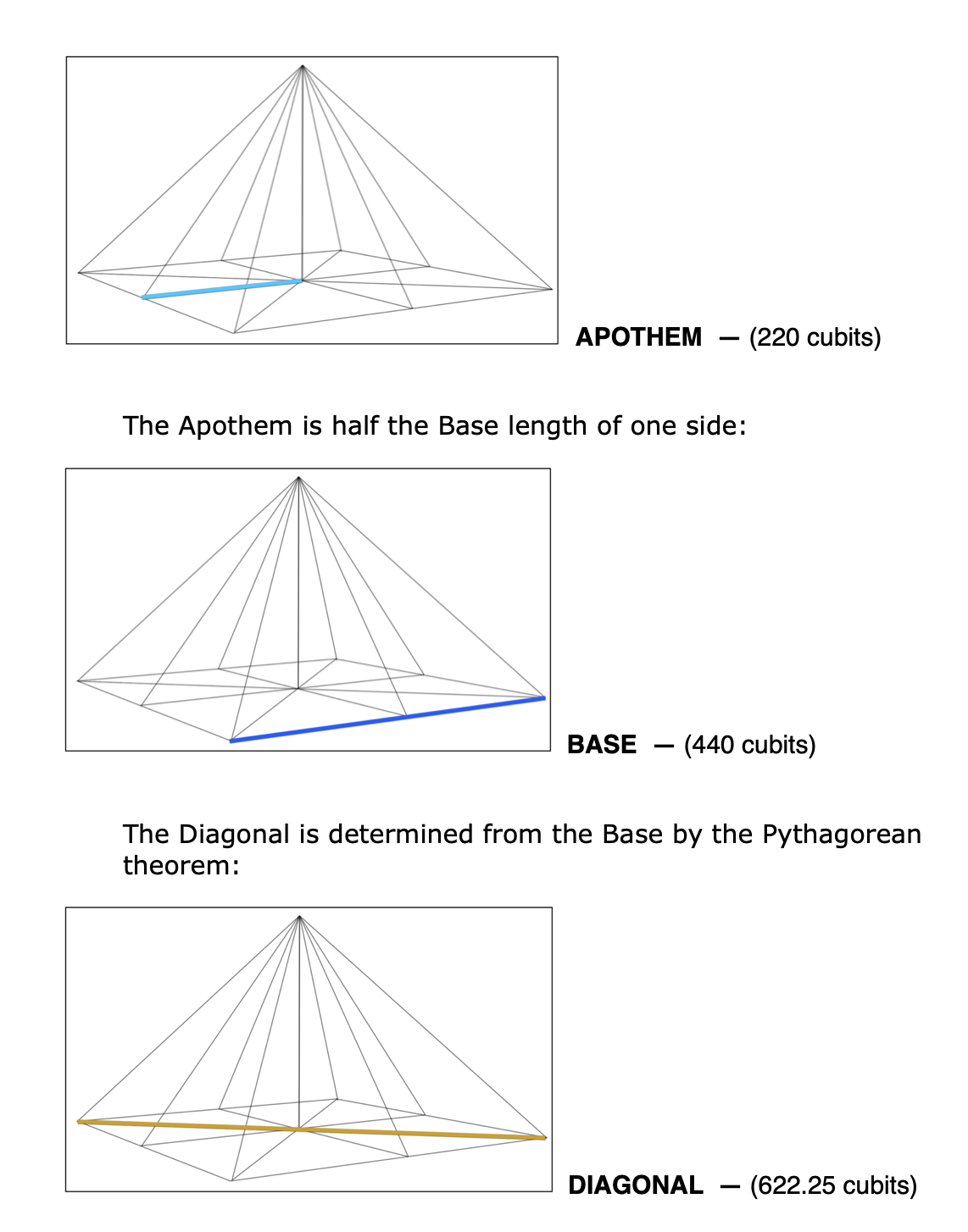
Given the average side slope angle of 51.845º, the remaining dimensions follow automatically:
Before we look at the pure, mathematical results it’s worth contemplating the deep, philosophical question underpinning this search. Why should we expect to find any constants miraculously hidden within these six proportions, which all result, after all, from one single piece of data, the side slope angle?
The Great Pyramid is utterly lacking in any of the hieroglyphic markings found on or within most Egyptian pyramids. Not a single symbol adorns the edifice, proclaiming its purpose. It has stood for thousands of years in mute testimony to… what? It beggars belief that a megalomaniac pharaoh, so intent on being immortalized that he had 100,000 slaves toil for twenty years to build the largest monument in the world, would not insist his name be all over the thing. Even if we assume his cartouches are missing because the limestone covering is gone, emblems celebrating his reign ought to be all along the inner grand gallery leading up to the famed King’s chamber where one would expect… well, a gold plaque at the very least! (Or was King Tut just a show-off?)
But no, there’s absolutely nothing. “Such heavenly touches ne’er toucht earthly faces.” How can this be? Unless we’re missing something right in front of our eyes?
What if its purpose is altogether different, as today’s alternative scholars insist (and Shakespeare seems to hint)?
Could its message be in the very form itself, inherent in the perfection of the geometry? If that’s the case we need look no further for the truth than the basic ratios that define its shape. And we should expect Einstein’s stated principle to apply: the truth must be beautiful and simple.
Just as we did with the hidden Sonnets lines, we shall apply only basic addition and division to the lines of the six basic pyramid dimensions. (As always you’re invited to double-check the numbers with a calculator, or watch the online video, or simply follow along and be amazed.)
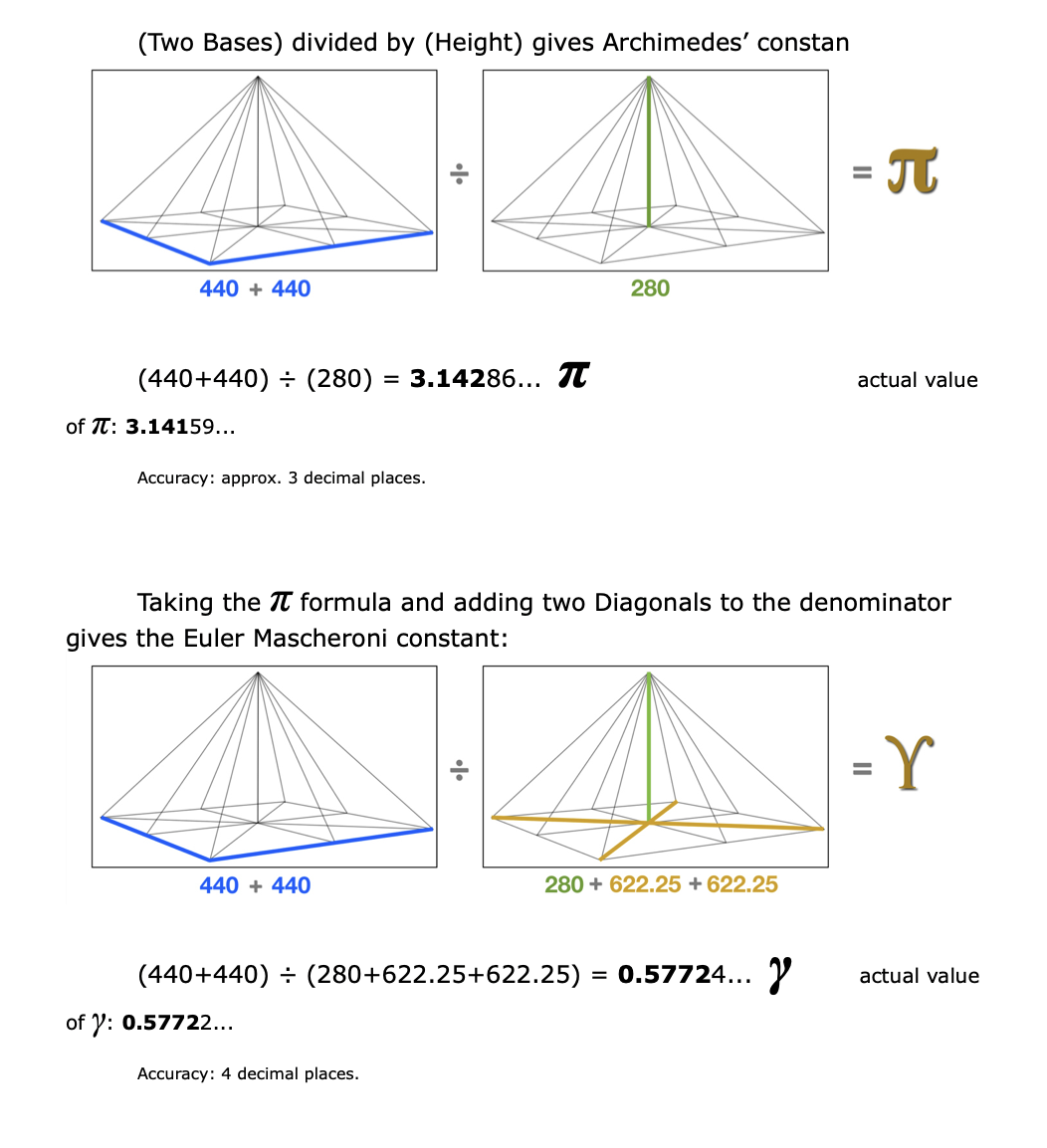
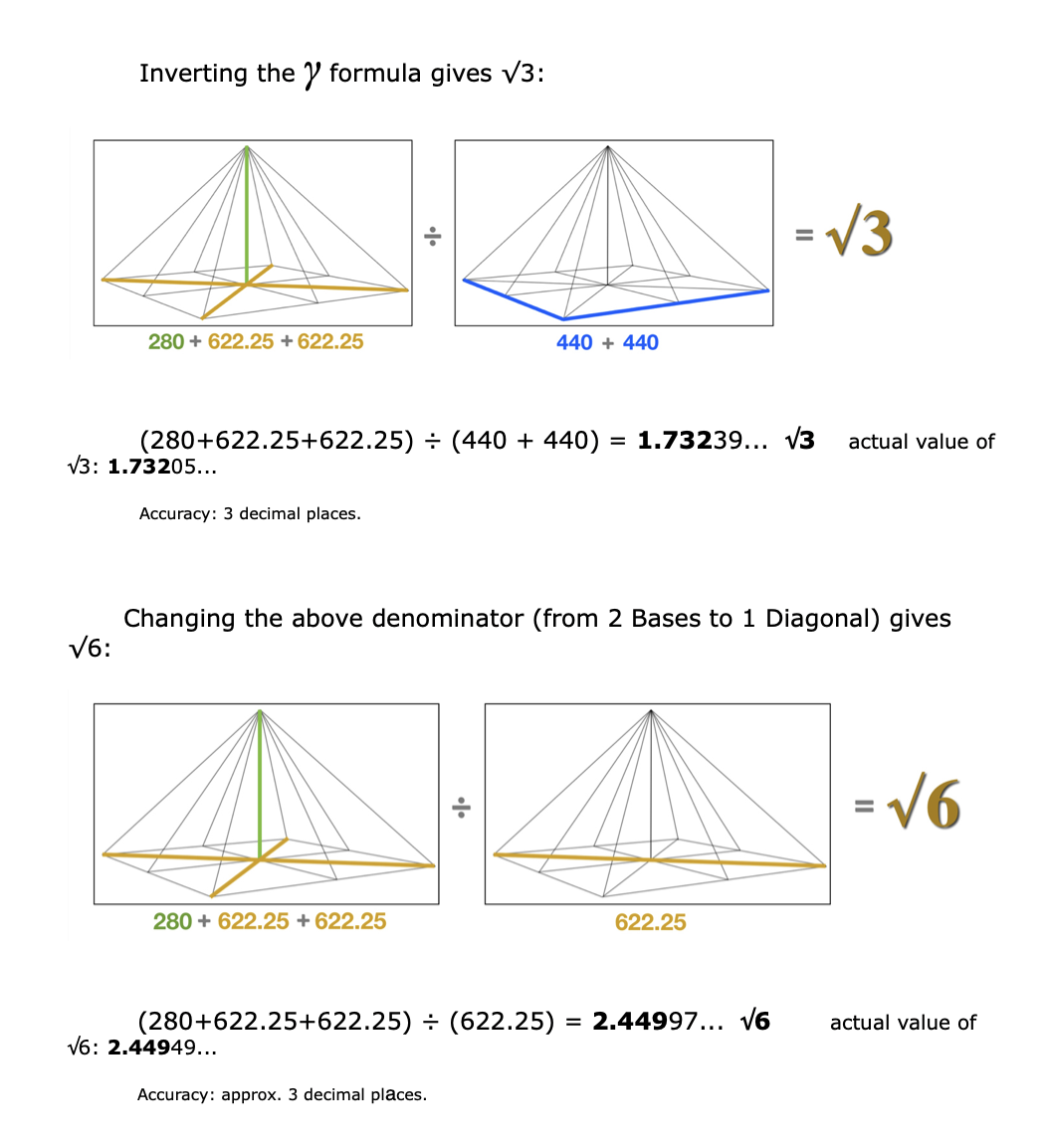
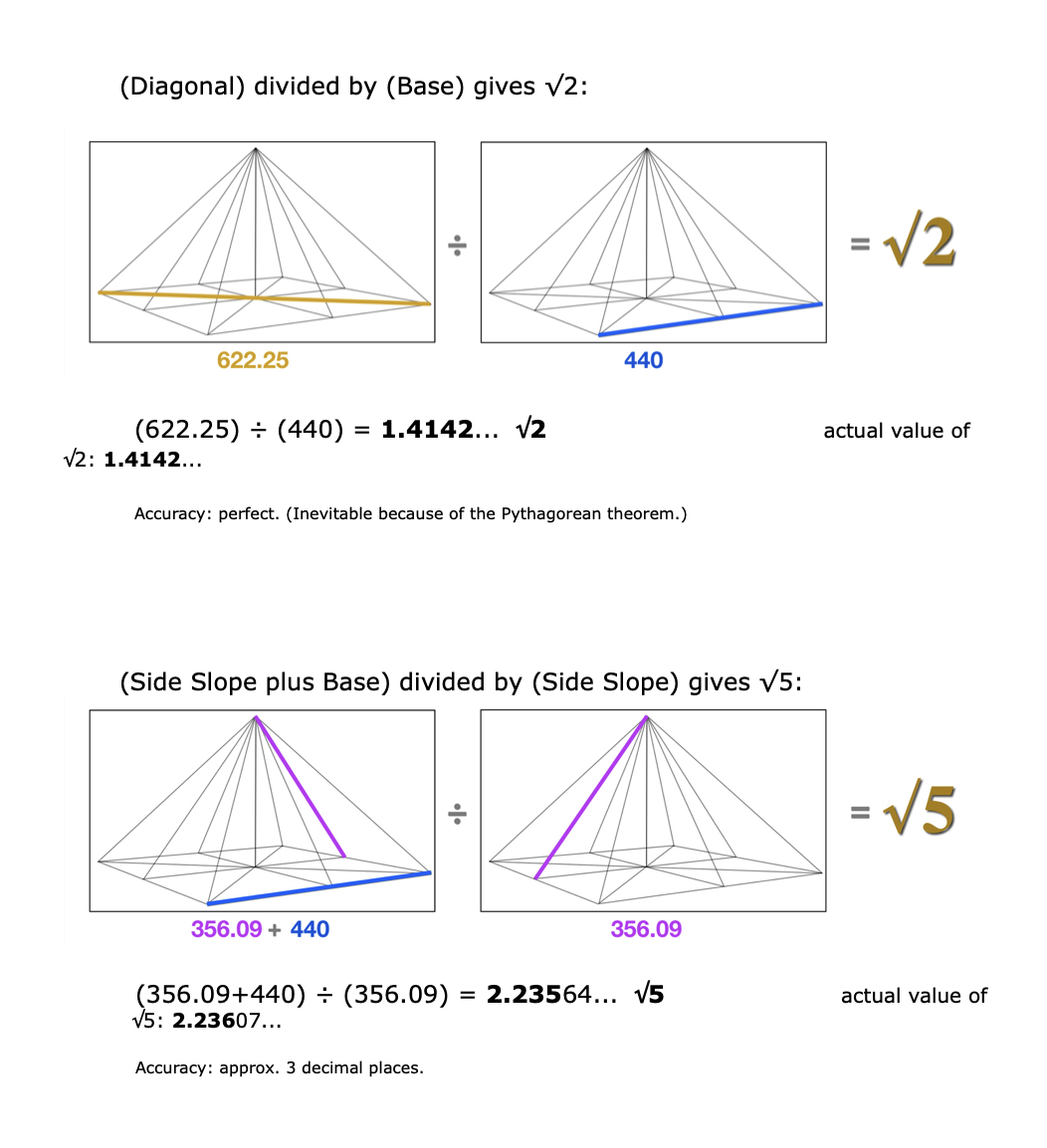
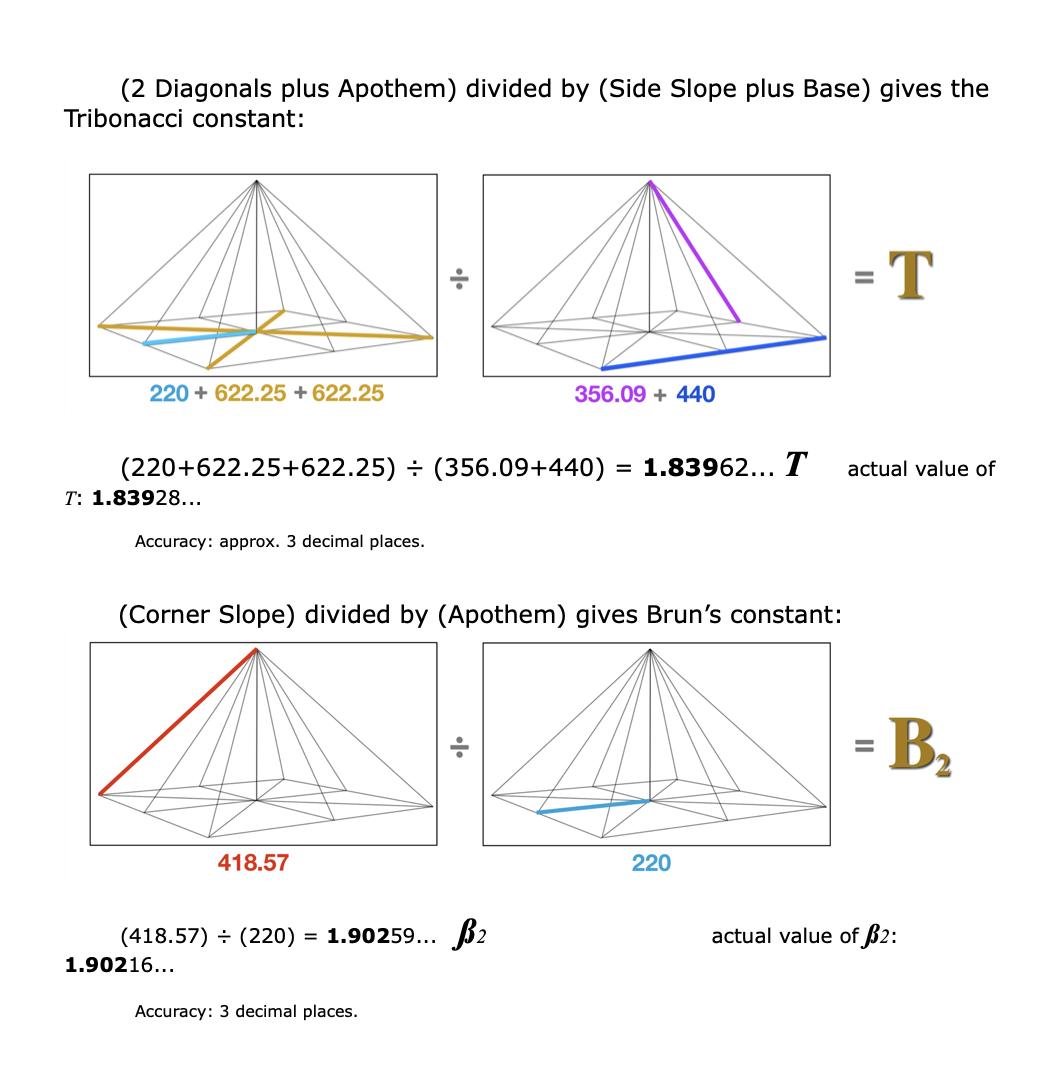
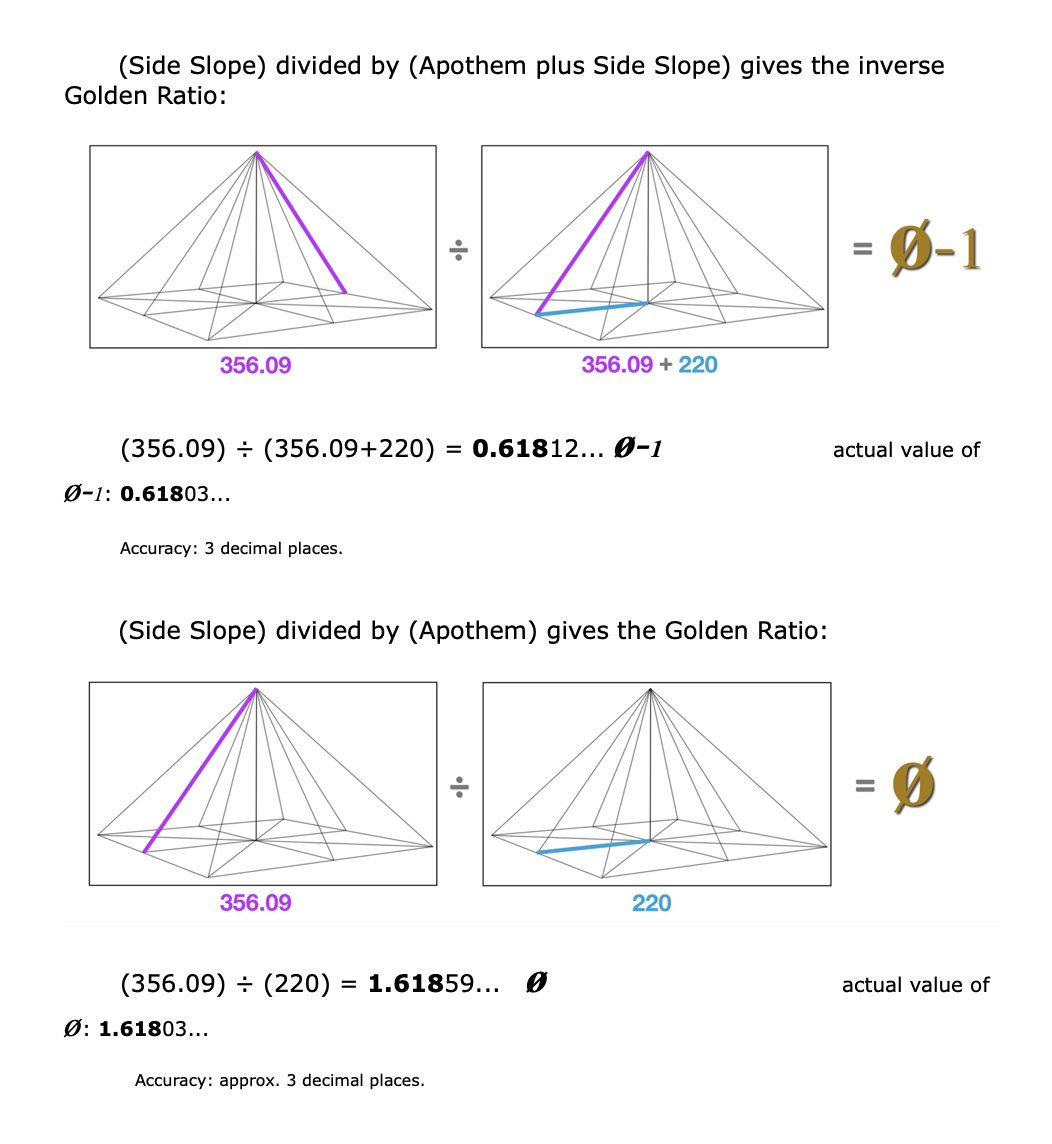
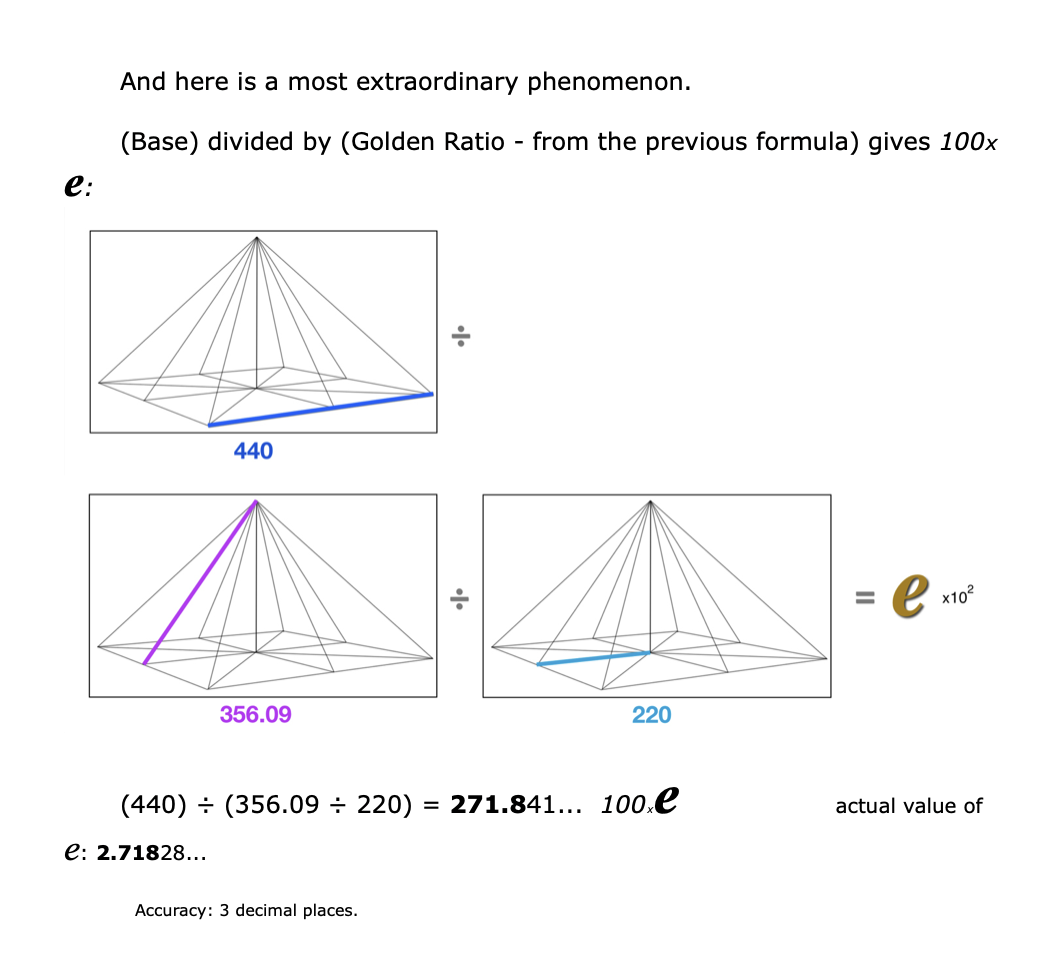
Skeptics may balk at this result, claiming that 100 x e is somehow not a legitimate proof of e’s presence in the pyramid. Perhaps another approach will help convince the naysayers.
Taking the results of Petrie (most respected of the earliest explorers), Lehner (most thorough of the moderns), and Cole (the official Egyptian Government survey) and using their average as our side slope angle, 51.8504º, gives the following:
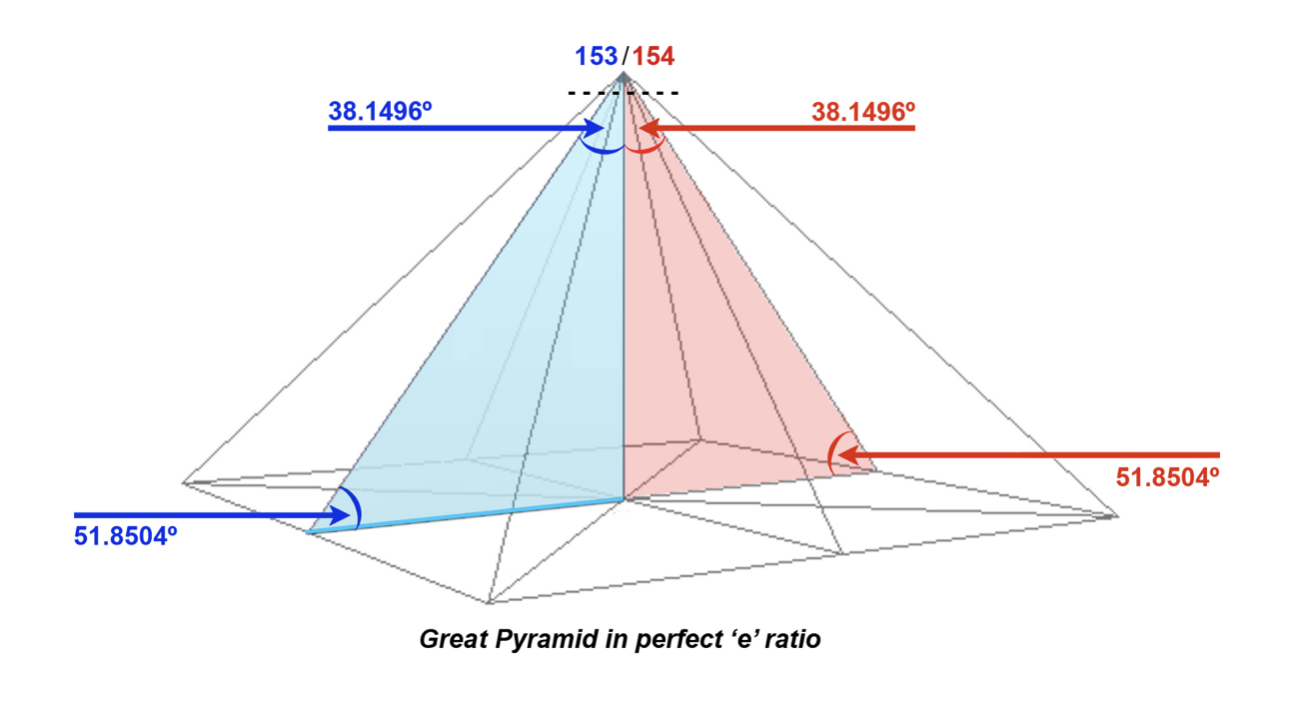
Given that the two base side slope angles are 51.8504º each, the capstone angles are therefore 38.1496º each. Using our Sonnets pyramid structure metaphor we’ll call the left side the ‘sonnet 153’ angle — and the right side the ‘sonnet 154’ angle.
Dividing the sonnet 153 side angles:
51.8504 ÷ 38.1496 = 1.359134…
Obviously dividing the sonnet 154 side angles gives the identical result. They seem to mean nothing in particular but adding the two sides together we get:
1.359134 + 1.359134 = 2.71827… which is e !
(The actual value of e = 2.71828 so this is accurate to almost 5 decimal places.)
Think for a moment what this means. The 153 side and 154 side each give a number that’s unrecognizable at first. But when added together (completing the overall capstone angle) they reveal one of the most important constants in mathematics.
Have we found the answer to why the poet has put two sonnets at the apex of his structure? Must the Bath sonnets be somehow joined together… a poetic metaphor for what the actual geometry of the pyramid capstone is hiding?
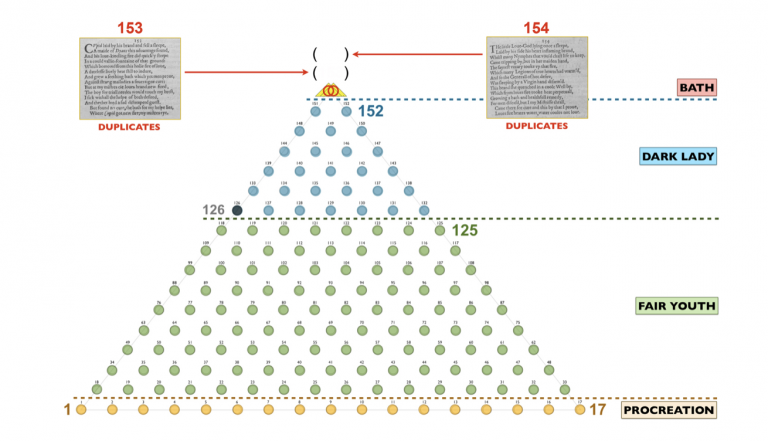
We’ve accounted for eleven of the twelve constants so far. It’s remarkable that despite the inevitable small inaccuracies inherent in the estimations of the original cubit measurements (to be expected after thousands of years of physical deterioration) the results are as precise as those revealed in the Sonnets title page… to around three decimal places or better.
Unfortunately for the Egyptologists this is a good news/bad news situation. The good news is it recognizes the extraordinary accuracy with which they’ve calculated the original dimensions. It’s an amazing feat of engineering and they should be congratulated for it. The bad news is that in order to continue defending their Khufu’s tomb story (and the timeline it depends upon) they’ll have to explain all over again about how the world was only just crawling out of the stone age; how they worked only with copper chisels, pounding stones, and woven ropes; how there was no wheel yet, but they had 100,000 slaves to whip it into shape. Yes, the Great Pyramid has been proven to be the most incredibly precise, mathematically significant edifice ever created, but not a single one of these constants could possibly have been intentional. It was all done entirely by accident!
Shakespeare, for one, would disagree, for he says in Sonnet 124:

“No, it was builded far from accident; It suffers not in smiling pomp, nor falls … But all alone stands hugely politic.”
It has no ostentatious cartouches, no lavish golden tomb. It falls not (though the region has been ravaged by earthquakes from time to time). It stands alone, unique in the world (politic here meaning shrewd, hiding its real meaning). Oh, and did he mention huge? It nor grows with heat nor drowns with showers (granite holds its form and hardly changes over aeons of heat or rain).
It should come as no surprise that we shall indeed find the twelfth constant, e-1, within these same pyramid ratios. This is the mysterious twin partner of e which was ignored by Isaac Newton yet showed up twice in the title page. The only one of the twelve constants the world is still unaware of today. Or perhaps I should say mathematicians are aware of it but only inasmuch as it relates to e. They don’t regard it as a significant constant in its own right.
The unexpected bonus of finding e-1 within the pyramid is that it opens up many other discoveries… as well as a pandora’s box of intrigue concerning the Universal Constant of Measure, present in the Sonnets title page and documented in detail in the video above.
… Stay tuned, there’s more to come.
