GREAT PYRAMID
Geographic coordinates of the Great Pyramid
I dare say the revelation in the YouTube video, BARDCODE: Sonnets Preview that’s the most difficult for people to wrap their heads around is the phenomenon of the latitude / longitude coordinates of the Great Pyramid.
As incredible as all the other mathematics on the Sonnets title page is, this is the one thing that seems to baffle people the most. Longitude was still a very imprecise science in 1609. Navigators could calculate latitude pretty well but Galileo was still wrestling with the longitude problem when he died, 25 years after Shakespeare’s passing
Yet if John Dee were really pointing us to the Great Pyramid (as so many other clues seem to suggest) his latitude/longitude coordinates are a staggering 99.999% and 99.99% accurate, respectively. It’s hard to argue against such precise evidence. And this is why the Greenwich problem is so confounding. Today we’re used to Greenwich being the location from where the world measures longitude; we don’t even think about it. But during the Renaissance there was no consensus yet on where the 0º meridian line should be. In fact the debate wasn’t settled until the International Prime Meridian Conference, held in Washington D.C., in 1884!
Most of us are unaware that John Dee literally wrote the book on The Perfect Arte of Navigation (1577). It was another of his areas of excellence on top of mathematics, cryptography, astrology, astronomy and… espionage! He worked tirelessly to get Queen Elizabeth I to adopt his theories on the subject. He’s generally credited with having coined the term ”British Empire”. Greenwich was the principal Tudor seat before Whitehall. Elizabeth was born there and it was her favourite residence. There’s no doubt that although it was not accepted by the rest of the world at the time, Dee clearly believed Greenwich was the only rightful meridian and the proper way of honouring his monarch. Since this question is so important, the only way I can address it properly is to link you to a portion of the relevant chapter from Book II, BARDCODE: The Missing ‘i’. You’ll find the link (to Greenwich Mystery) at the end of this section.
Meanwhile let’s address the primary concern: the detailed mathematics that produces the pyramid’s precise coordinates. As seen in Diagram 1, the angle that reveals the latitude is very simple to find.
Diagram 1:

A line is drawn horizontally as a baseline from the G dot, through the T. T. dots, to the point M, where CM is a perpendicular dropped from C.
The right triangle GMC is thus formed and the software measures GM to be 31.14 and CM to be 17.96. The Pythagorean Theory (a2 + b2 = c2) holds for the triangle, assuring its accuracy.
It’s now a simple matter to calculate the cosine for ⦟CGM: 31.14 ÷ 35.95 = 0.866203 which gives ⦟CGM as 29.9796º.
As seen in Diagram 2, however, finding the angle that reveals the longitude coordinate is more complicated.
Diagram 2:

Here we see tangent line GL (at right angles to hypotenuse GB) in triangle GLB (that revealed √5 and √6). GA is part of triangle GAB that gave us e-1. (See the last diagram on Sonnets Math (Main) or individual triangle diagrams in Triangle Math Diagrams.)
Note that triangle GLA is not a right triangle. In order to create an easy way to measure ⦟ LGA we must extend GA out to meet a line drawn from L, parallel to the hypotenuse, GB.
We shall call this new point, A+. And the new G point we’ll call G-.
Diagram 3:

The software now reveals the following measurements:
LA+ = 10.08
G-A+ = 19.50
(Longer than GA because the line has had to be extended past A.)
LG- = 16.69
(Shorter than the previous GL because the line crosses GA+ to the left of where it formerly landed on G… hence, G-.)
This is easier to comprehend if we examine the following close-up diagrams.
Below we see a close-up of the original line GA (aqua – measuring 18.98) as it appears in triangle GAB (which gives us e-1).
Also we see the original line GL (black – measuring 16.90) as it appears in triangle GLB (which gives us √5 and √6).
Diagram 2 (close-up)
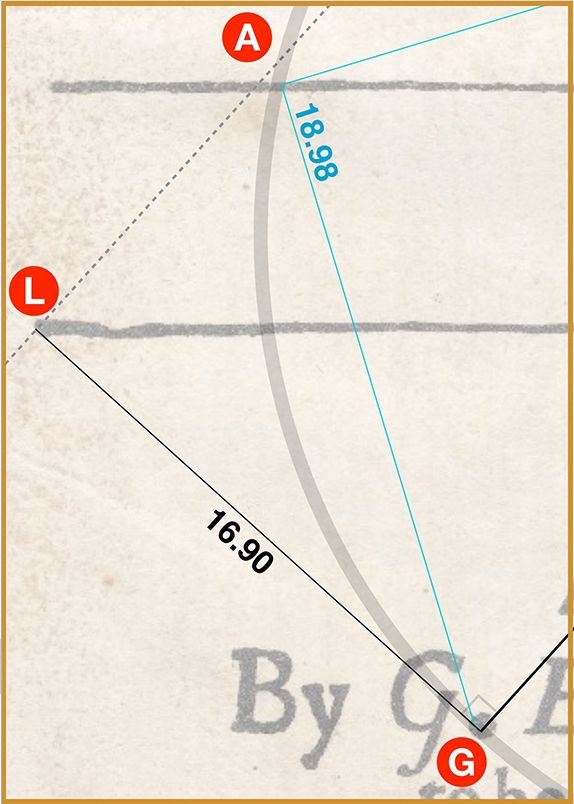
Note that the aqua and black lines land on different parts of the large G dot… but both within the dot and on the circle’s circumference.
Clearly if we are to find the accurate ⦟ LGA we must measure it from where these two lines intersect on the G dot.
This is going to change the length of LG even though the point L remains the same. It’s now LG-. It’s also going to change the length of GA, to GA+, as previously shown in Diagram 3.
Diagram 3 (again):

In fact we have to extend it to a point A+ as shown in the next close-up, so as to form a perfect right angled triangle,
LG-A+.
Diagram 3 (close-up)
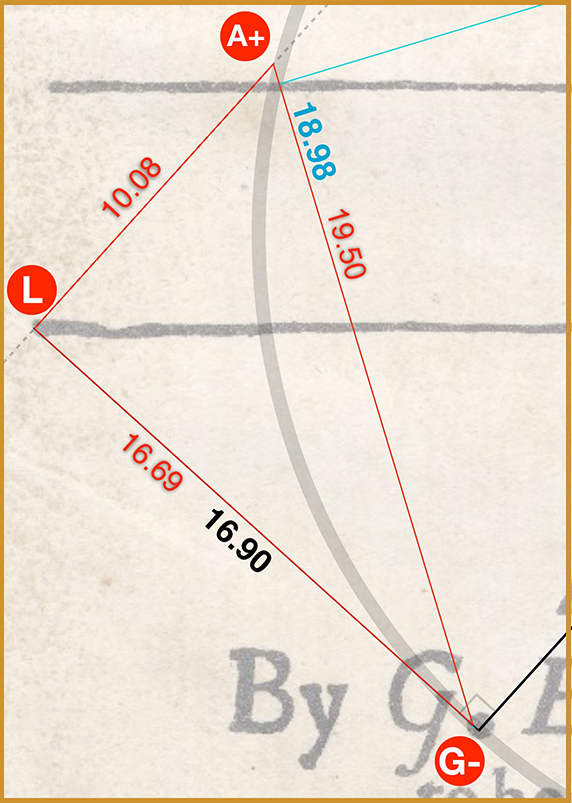
Note how the red lines are overlaid onto the aqua and black lines at their point of intersection — still within the G dot and on the circumference. We’ve done nothing to interfere with the original lines GL and GA. Their relative angle is identical. In other words:
⦟ LG-A+ is still the same as the original ⦟ LGA.
We’ve simply found their point of intersection in order to create a perfect right triangle, LG-A+, so we can more easily calculate the angle.
As previously noted the software gives the following measurements:
LA+ = 10.08
G-A+ = 19.50
LG- = 16.69
As with triangle GCM in Diagram 1, the Pythagorean Theory (a2 + b2 = c2) holds for triangle LG-A+, assuring us of its accuracy.
It’s now a simple matter to calculate the tangent for ⦟LG-A+:
10.08 ÷ 16.69 = 0.60395 which gives ⦟LG-A+ as 31.1299º.
These two angles are, of course, the latitude (29.9796º N.) and longitude (31.1299º E.) coordinates revealed in the BARDCODE: Sonnets Preview

Click here to continue to Triangle Math Diagrams for detailed diagrams of the precise measurements of each triangle revealed in the Sonnets title page.
