
THE GREAT PYRAMID
Why is Shakespeare insisting we look at Giza?
The Great Pyramid of Giza is the oldest man-made structure on earth, the last survivor of the Seven Wonders Of The Ancient World. The massive monument comprises 2.3 millions stones weighing 6.5 million tons sitting on a square base the size of six football fields. The average weight of each limestone block is over 2.5 tons and they’re laid in such near-perfect alignment with true north that we couldn’t match their precision today. Larger granite blocks that make up the inner King’s Chamber, weigh between 50 and 80 tons each and are cut so perfectly you can’t slide a razor blade between them.
Named after the Fourth Dynasty pharaoh, Khufu (circa 2600~2500 BCE), Egyptologists insist it was constructed solely to be his tomb. But no mummified remains have ever been found inside any Egyptian pyramid so non-traditional scholars conclude they had an altogether different purpose. Given the phenomenal accuracy with which the Great Pyramid was built many are convinced it dates from a remote golden age when higher mathematics and art, they believe, were combined to convey divine principles.

Based on Khufu’s known lifespan the official party line is the structure had to have been completed in twenty years otherwise the tomb story doesn’t work. But even with a maximum possible 16-hour shift every single day for 20 years (assuming there were no flood-lights for night work) it would require quarrying, transporting, dressing and precision-placing one Cadillac-sized stone every three minutes! But that’s impossible! So something has to be adjusted to make the math fit, hence the story we all learned in school: it was done with the forced labor of 100,000 slaves. We’re not told how they organized such a logistical nightmare, of course. The porta-potty situation, for instance?
But leave that as unsolvable for now. What’s of interest here is why Shakespeare (with John Dee, on his behalf) performed the almost inconceivable task of encoding the geographic coordinates of the Giza complex into the punctuation on the Sonnets title page. If you haven’t already seen the full BARDCODE Sonnets Preview video under the Mystery menu, check it out. But here’s a short-cut to the Grand Finale:
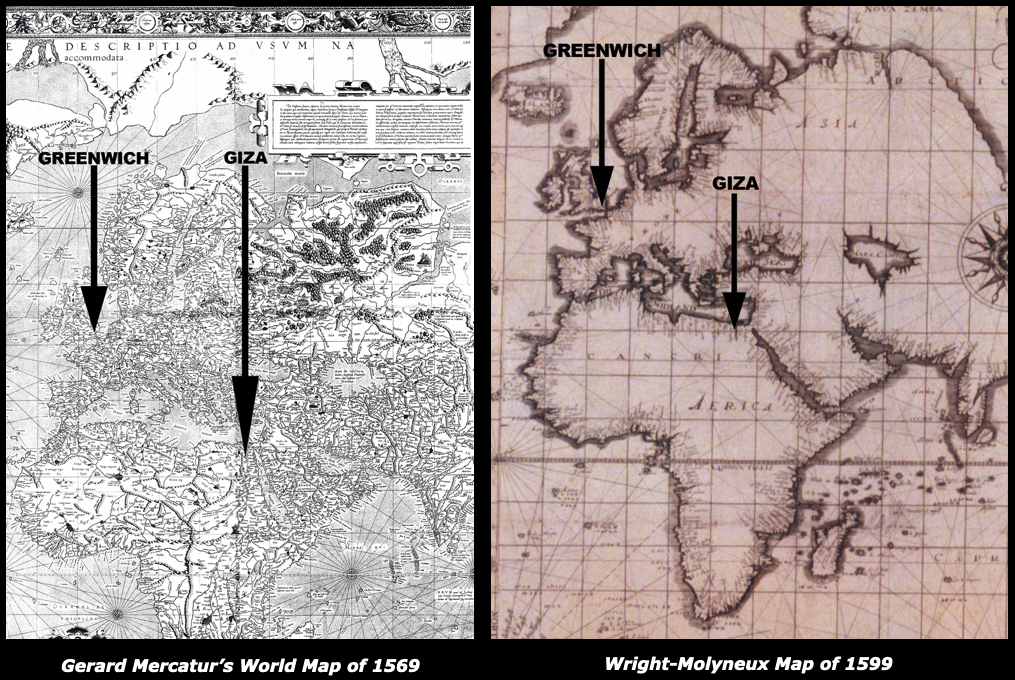
So how impossible is what you just saw? Notice the latitude is practically spot on… mere feet north of the exact centre line of the pyramid. It’s 99.999% accurate, in fact! The longitude is off by about 350 yards from centre (99.99%). But we need to understand that in 1609 the science of how to calculate longitude was not even known. Galileo was still wrestling with the problem when he died 25 years after Shakespeare’s passing.
In 1599 the Wright-Molyneux Map was hailed both for its extraordinary accuracy and honesty. Where previous cartographers had put in all kinds of wild, squiggly speculation whenever coastline details were still unknown, Wright had truthfully depicted hundreds of miles with straight lines indicating, in effect… we just don’t know yet. (Shakespeare shows he’s aware of this by having Maria joke about Malvolio, in Twelfth Night : “He does smile his face into more lynes, then is in the new Mappe, with the augmentation of the Indies.” In other words he smiles but doesn’t know a thing!)
Nevertheless, despite the Wright-Molyneux’s extraordinary accuracy, the longitude settings between Greenwich and Giza were still off by 1º, which translates to about 70 miles on the ground. The idea that in 1609 anyone could calculate longitude accurate to within 350 yards of the pyramid’s centre is frankly astonishing.

What makes this all the more astounding is that when Shakespeare’s Sonnets was published in 1609 the world was in complete ignorance about pyramids in general. These engravings (from before, during, and long after the poet’s life) show various artists’ impressions of what they believed the pyramids looked like.

The first book on the subject, Pyramidographia, by John Greaves, wasn’t published until 1646… thirty years after Shakespeare’s ‘official’ death. And it wasn’t until 1836 that Colonel Howard Vyse published the first accurate measurements of the pyramid. They attracted the attention of the publisher of London Magazine, John Taylor, who in 1859 published The Great Pyramid; Why Was it Built: and Who Built it?, in which he speculated about close correlations between the pyramid’s proportions and the math constants Pi and Phi.
Yet all that (and far more!) had already been brilliantly encoded in 1609 using just four dots and two lines.

Unknown longitude? Unknown constants? Unknown pyramid dimensions? And then there’s the fact that Greenwich would not be established as the Prime Meridian until 1884! What on earth are we dealing with here?

THE GREENWICH MYSTERY
John Dee's intended centre of the British Empire
(and the Queen's favorite residence)
There’s a far more esoteric level of impossibility going on here than meets the eye. Look closely at the longitude lines in the two most accurate maps of the period. It’s unclear where the 0º Prime Meridian point is located but you can see that none of the vertical meridians is going directly through Greenwich. That’s because no uniform 0º position had yet been established from which to measure longitude east or west. Generally it was from a position about 25º west of Greenwich, but even that varied as the science of navigation was in its infancy and territories argued endlessly over who had the right to choose. Politics and diplomacy moved at a glacial pace and Greenwich wasn’t selected as the 0º longitude location until the International Prime Meridian Conference, held in Washington D.C., in 1884!
So what’s going on? Obviously there will be those who’ll claim that because Greenwich was not the Prime Meridian location back then this discovery of a 31.1299º latitude angle is meaningless; it couldn’t possibly have been intentional. But there’s far more going on here and the plot thickens. In 1582/83 John Dee wrote a very detailed but cryptically dense, 62-page proposal called “A Plain Discourse … concerning the needful Reformation of the Vulgar Calendar”. In it he was lobbying the Queen to adopt his own variant of the new Gregorian calendar which had recently reformed the old Julian by a 10-day shift intended to re-align Easter properly with the movements of the heavens and modify the leap year system to keep it aligned. Dee proposed an 11-day shift (which we now know would have proven vastly superior) but there were ecclesiastical objections lodged by bishops and ultimately it was never approved. But for political and national security reasons the astronomical mathematics behind Dee’s plan had to be kept secret because it involved possible military action to take possession of what Dee himself believed was “God’s Longitude”.

It appears that by 1582 Dee may have already mastered the longitude problem via a method unknown to us today. (It’s a subject I discuss in my third book, The Shakespeare Equation.) But whether or not that can be proven it’s clear Dee’s calculations centred around the absolute necessity of Greenwich being the prime meridian and thus London, the axis of the New World. Dee used a 33-year structure of leap years modeled on Jesus Christ being 33 when crucified. And because this small variation of the Gregorian solution resulted in a vastly more accurate long-term calendar, Dee was convinced this was the perfect mathematical order of Nature itself. To him it was literally written in the stars that Greenwich (which happened to be Queen Elizabeth’s favorite palace residence) was the divinely ordained centre of the globe. The place where time itself begins and ends! He would’ve calculated the pyramids’ longitude from Greenwich whether or not the world eventually recognized it.

As it turned out Greenwich was not recognized as the 0º reference point of time and longitudinal position until 275 years after Dee’s death. So I empathize completely with all those who find this to be a stumbling block to acceptance of intentionality. I wrestled with this myself from the moment I first discovered those two angles landed us precisely at Giza. It boggles the mind because the rest of the geometry is so slam dunk it’s beyond argument. You can say you don’t understand it – or even don’t like it – but you can’t deny it’s there. Nevertheless this seemed even more impossible than the rest until I fully understood Dee’s colony-building mind-set and the need for national secrecy concerning his push for building a British Empire!
But if that’s not enough to sway a doubtful mind I ask only that you suspend disbelief for just a moment and examine every other option that was possible at the time.
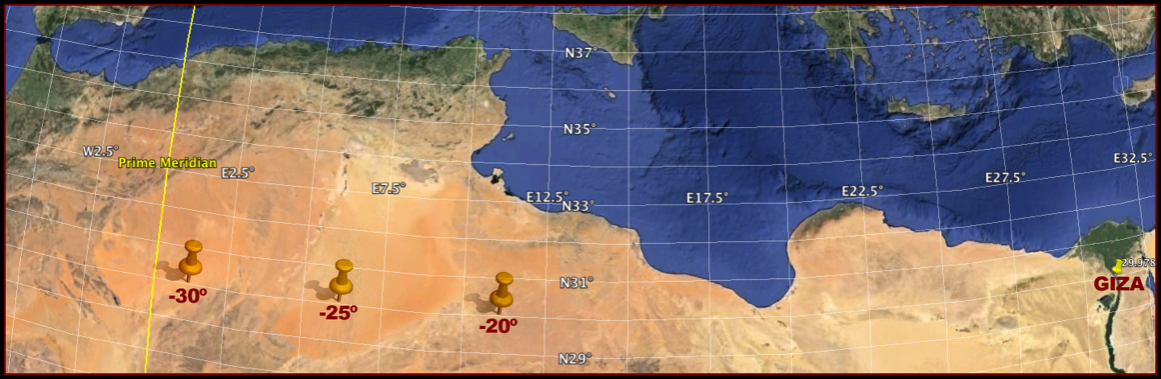
In the Google Earth map above the pins indicate the other popular prime meridian contenders of the 16th and 17th centuries and where they would’ve ended up pointing to if Dee had used those instead of Greenwich. The most common was about -25º west of Greenwich. So 31.1299º east of that meridian would have led us directly to… sand! The other common variant was about -20º west of Greenwich. It points to… sand again. As does -30º. In fact, pick any possible place in the known world at the time from -1º west of Greenwich all the way to about-40ºwest. For 2,500 miles straight west of Giza there’s not a town, a river, a lake, a forest, or a Pizza Hut.* It’s just sand all the way and after that, the Atlantic… for about three thousand miles to a world they could not imagine.
*I’m pretty sure the very last Pizza Hut is right there at the Giza plateau!

So before you bury your head in everything west of the pyramids. Or drown. Ask yourself a few basic questions:
Would someone so brilliant as to have created the undeniable masterpiece of geometry you just saw on the Sonnets title page… would he then jump through hermetic hoops to point us to a pile of sand or an ocean of brine? It’s a serious question because if you want to deny intention concerning the exact latitude and longitude of Giza you have to deny the obvious intention involved in precisely defining the ‘twin pairs’ constants (e /e-1), (ø /ø-1), (γ /√3), the ‘twin Theodorus’ constants (√3 /√2), (√6 /√5), and the ‘twin primes’ constant, ß2. Why are they all twin mathematical relationships? (How often does Shakespeare use the metaphor of mistaken identity between twins?) You have to ask yourself would someone who knew how to interweave all those connections into a 3:4:5 triangle (to an accuracy of three decimals). Someone who could cryptographically embed two angles to reveal a very special latitude and longitude… would he do it to point out some sand or water in the middle of nowhere?
Or, after encrypting the obvious clue of a visual representation of The Theorem of Thales (the first person to measure the height of the Great Pyramid), is it more likely that this is his message?

All we know for sure is that this phenomenon, whatever it is, is profoundly accurate, beautiful, and provocative. John Dee (or Shakespeare) ((or someone!)) went to incomprehensible lengths to calculate and design all this and then hide it for “eyes not yet created” (sonnet 81). We should probably take it seriously. Because clearly there really are more things in heaven and earth, Horatio, than are dreamed of in our philosophy.
