SONNETS MATH (MAIN)
The Numbers
GEB is a 3:4:5 triangle so the position of E is non-negotiable. There are only two positions on the right of the hypotenuse where it can land. Once having decided on this position, Dee’s choices in fitting everything else around it are largely predetermined.
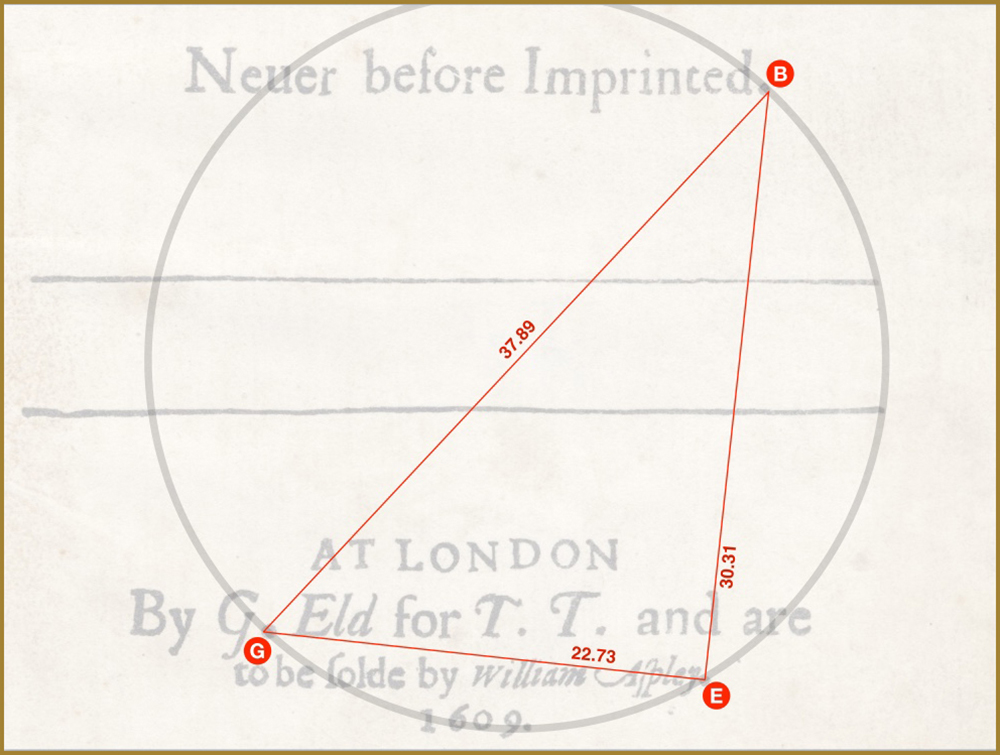
For instance, GE is part of the ø and φ ( ø-1 ) calculation. It must be in perfect golden ratio with GF so consequently the position of F is also non-negotiable.
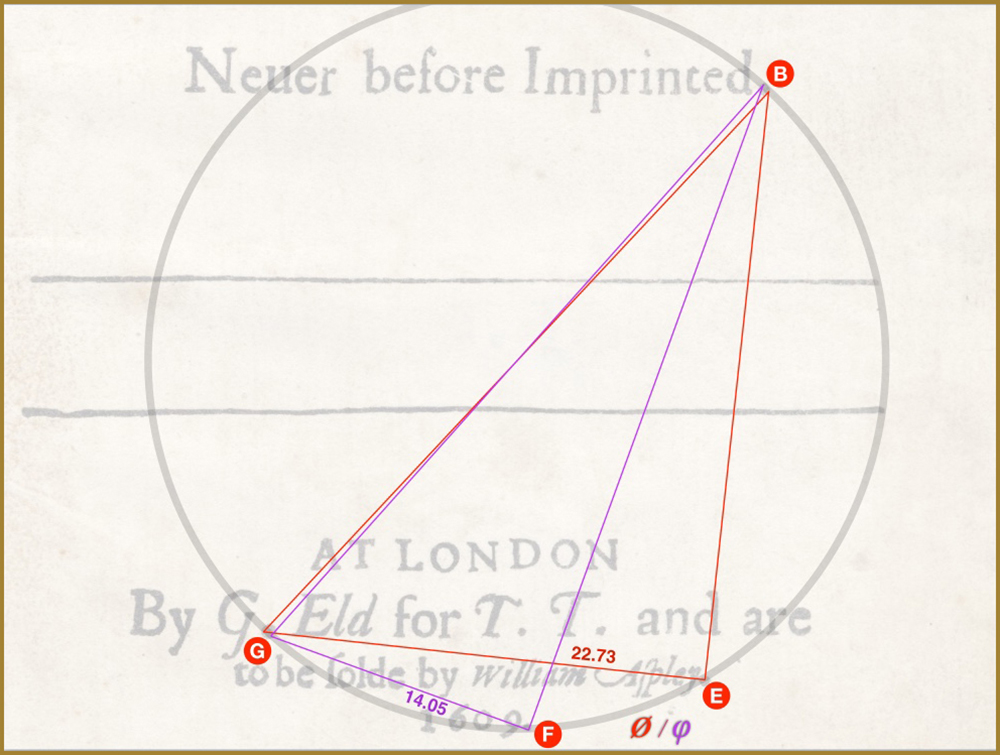
Technically they could both share a common hypotenuse at this point but one of them would have to tilt over towards the other, resulting in either the Aspley dot or the 1609 dot having to move slightly. But Dee is the leading mathematician, geometer, cryptographer of the Renaissance; he has a lot more math wizardry up his sleeve.
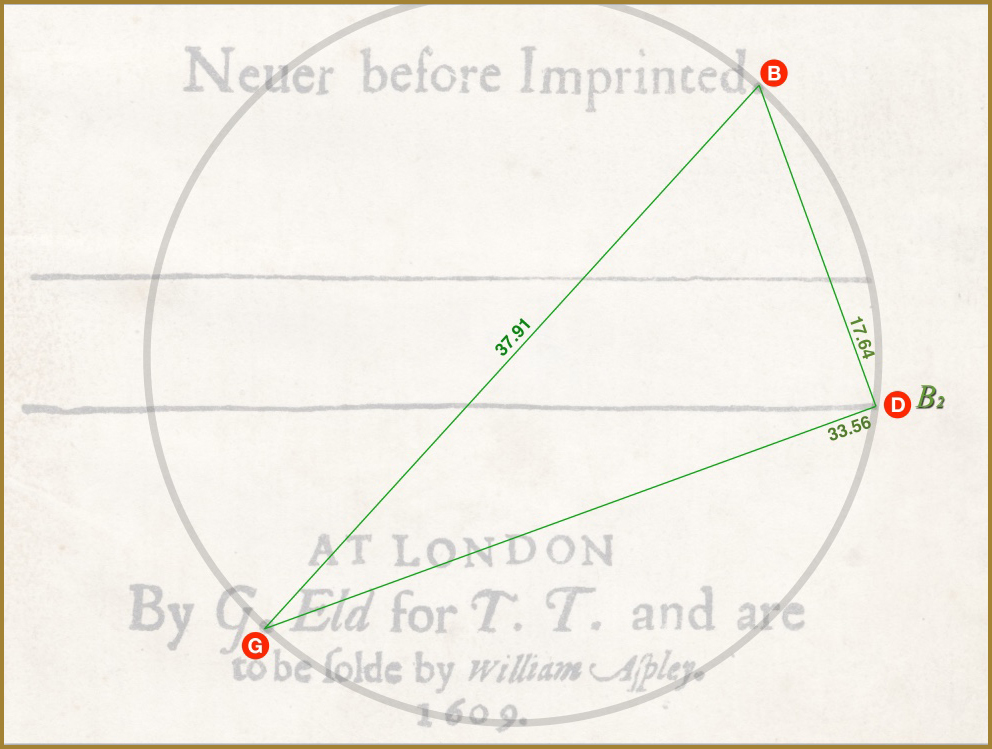
Triangle GBD gives us Brun’s constant, B2, so the position of D is also non-negotiable. But even at this stage it too could share the same common hypotenuse. BD and BG would have to be minutely shorter and the lower horizontal line would have to move a bit but it could be done.
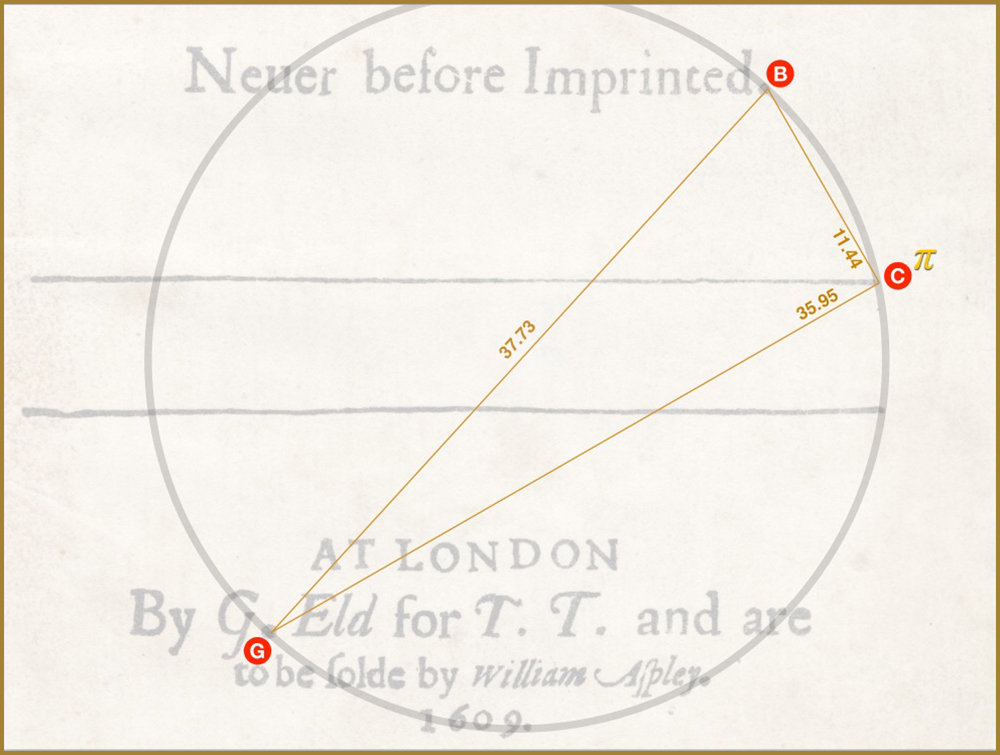
Finally, triangle GBC could also join the group, though BC and GC would have to be slightly longer and C, whose position is also non-negotiable if it is to give us π, would likely mean moving the top horizontal line a smidge. But again, it’s possible.
That’s the limit, though. Three constants plus a 3:4:5 triangle. And if this were all Dee wanted to do he could’ve accomplished it by shifting the Aspley/1609 dots and the horizontal lines just slightly and making the G/Imprinted dots regular-sized.
Today, any high-school kid with a pair of compasses and a ruler could get this far. Dee, however, wanted to embed far deeper relationships into his masterpiece; concepts I couldn’t reveal in the BARDCODE video because they would’ve overwhelmed a general audience.
But you, dear reader, are a true geek. You came to the MATH tab! So buckle up and enjoy the ride.
Discovery 4: Bringing proper tools and rigour to bear on the problem we see, from the following diagram (and the related pages under The Sonnets / The Math sub-menu) that all the calculations are accurate to at least three decimal places.
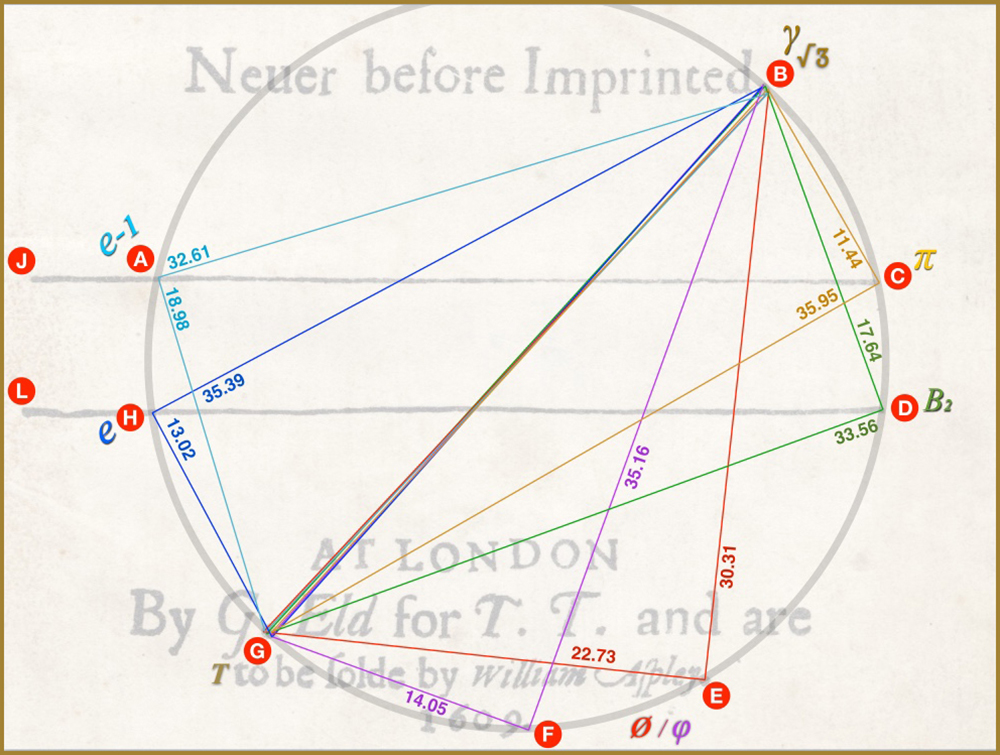
We just saw that the position of D is non-negotiable because BD/GD gives us Brun’s constant to 3 decimals.
Yet D is inextricably connected to H via the lower horizontal line DHL.
And the position of H is non-negotiable because its triangle, GBH, gives us e to 3 decimals.
But H is inextricably connected to A because its triangle, GBA, gives us e-1, also to 3 decimals. So the horizontal lines cannot be moved (at least not in relation to each other).
And yet A is inextricably connected to C via the upper horizontal line, JAC.
And C’s position is non-negotiable because its triangle gives us π to 3 decimals, remember?
So A, C, D, and H are absolutely interdependent.
Stop and pause to think what this implies and you begin to get a glimpse of what Dee is showing us here. These four points, in effect, cannot be anywhere else! It means there’s a presently unknown connection between the four constants they represent.
It’s the same for E and F and the 3:4:5 triangle. They cannot be anywhere else in relationship to each other.
But now we’re about to fall down a rabbit hole deeper than we ever imagined because…

BE divided by BD gives us e-1. To 3 decimals.
And BE plus BD, divided by BD gives us e. To 3 decimals.
So this connects both groups together. Time to pause and think again.
The stunning implication is that everything is inextricably connected to everything else!
At this point you’d think Dee would’ve reached the limit of his geometric mastery. We’ve seen him manipulate arguably the five most important math constants — π, ø and ø-1, e and e-1, — into an elegant interconnected web surrounding the Pythagorean 3:4:5 triangle. Plus, of course, Brun’s constant ß2.
But our rational minds compel us to dismiss this, at least momentarily, because the latter three of these were not known in 1609. ß2 (the converging limit of the sum of inverse twin primes) wasn’t calculated until 1919! Euler’s Number, e, came via Newton in 1669 (and Jacob Bernoulli in 1683) and neither recognized e-1 as significant. (That’s harder to dismiss though, because they each occur twice.)
But there’s a deeper message here because all three of these supposedly unknowns (ß2, e, and e-1) are also to be found in the basic proportions of the Great Pyramid of Giza. And thanks to several clues placed throughout this masterpiece, it’s clear the encryptor is, in fact, pointing precisely to that last surviving Wonder of the Ancient World!
It begins to look as though John Dee’s purported connections to the secret society of Rosicrucians (and their reputation as a conduit of Ancient Egyptological wisdom) may be the solution to this mind-boggling puzzle.
That discussion is taken up in Book II, BARDCODE — The Missing ‘i’. For now we must move on to other treasures Dee has left for us.
The mystery of the common hypotenuse
So far he’s used the tiny length and angle differences of six hypotenuse lengths (along with exaggerated dot sizes at ‘G’ and ‘Imprinted’) to give us six constants. Using the same triangle line lengths and a common average hypotenuse, a further six constants will now be revealed.
The hypotenuse value of 37.79 is the average of all the hypotenuse lengths associated with the various constants. Their individual measurements are given in detail in several other pages files available under this Math menu. But for ease of reference they’re also tabulated here:
| △ colour | constant | value |
| yellow | π | 37.73 |
| dark blue | e | 37.71 |
| light blue | e-1 | 37.73 |
| green | B2 (Bruns) | 37.91 |
| mixture | γ (Gamma) | 37.79 |
| mixture | √3 | 37.79 |
| mixture | T | 37.79 |
| black | √5 | 37.79 |
| red | 3:4:5 | 37.89 |
| average | – | 37.79 |
| none* | ϕ | — |
| none* | φ | — |
| none* | √2 | — |
| none* | √6 | — |
*No hypotenuse is required for calculating phi (ϕ), phi-1 (φ), √2, and √6
Continuing our contemplation of the interconnectedness of this web of constants:
BE and BF, in relation to the average (37.79) ‘common’ hypotenuse, GB, gives us √3 AND… the Euler-Mascheroni constant, γ. Both to 3 decimals.
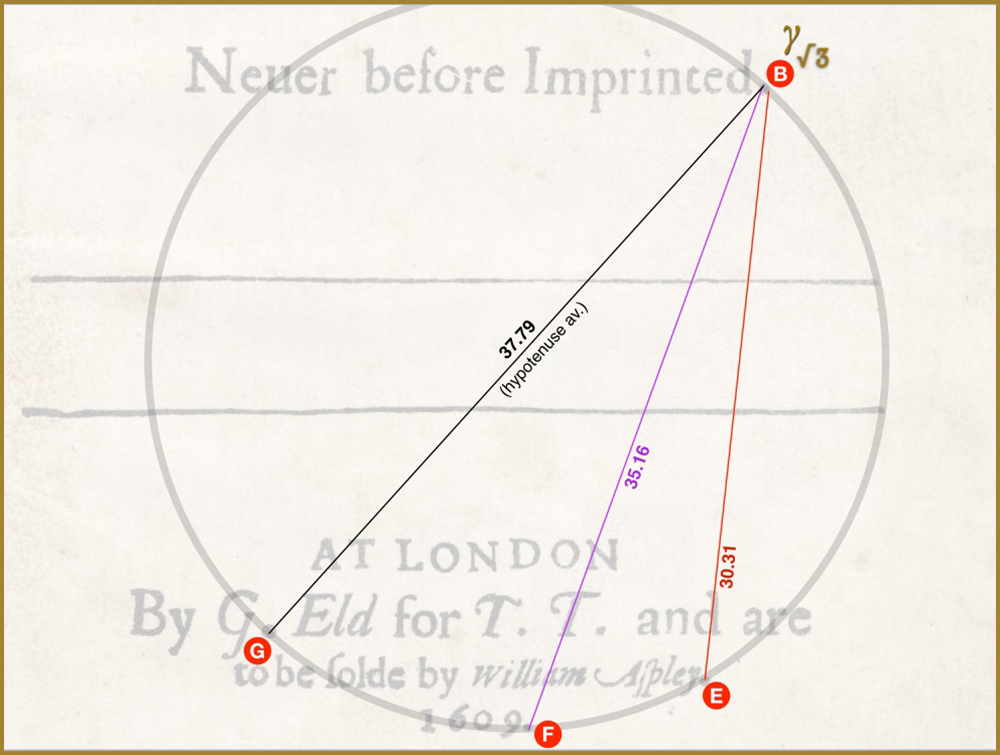
And GC and GD (also in relation to the average ‘common’ hypotenuse GB) give us the Tribonacci constant, T, to 3 decimals.
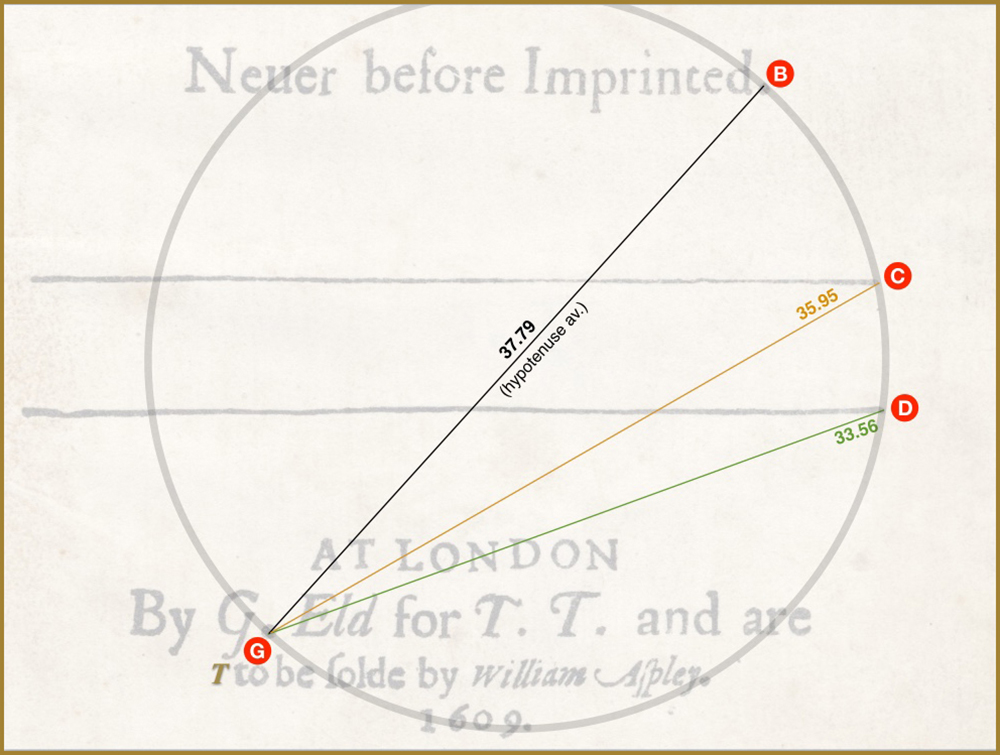
Are we getting the picture yet?
Throw in two more versions of ø and ø-1 PLUS… √2, √5, and √6 and we’re just beginning to glimpse the enormity of what Dee has done. (For more detailed imagery of ALL the constants see the individual pdf files under the MATH tab.)
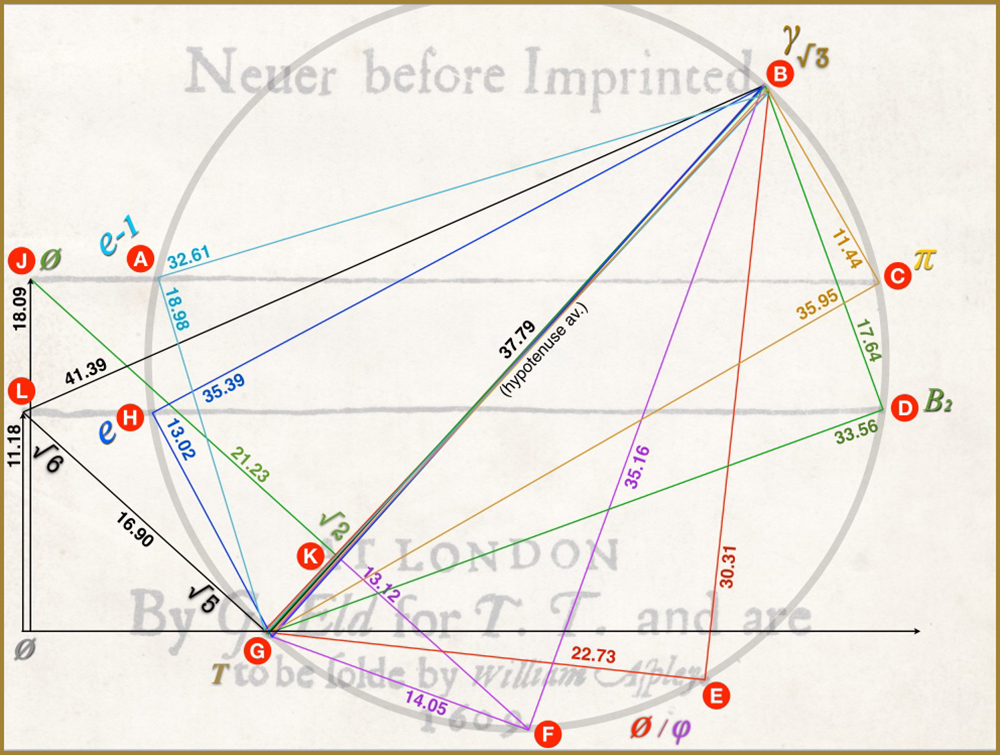
π, √2; √5 and √6; √3 and γ; e and e-1 (twice); ø and ø-1 (three times); ß2; T.
Twelve individual constants. Five unknown at the time. Four twin sets impeccably balancing each other (with two sets repeated multiple times). Fibonacci mirrored by Tribonacci. All interconnecting and centered around the iconic 3:4:5 triangle.
Summing up
Discovery 5: Ultimately 12 of the world’s most significant math constants are secretly represented by the judicious placement of just four dots and two horizontal lines.
Add to this…
Discovery 6: The long-sought ‘Universal Constant of Measure’ (which Newton spent his life trying to prove) is revealed in three of the Sonnets triangles. Newton was searching for the Foot / Cubit relationship but this reveals the infinitely more elegant Foot / Cubit / Metre relationship which I unveiled at the 2016 CPAK conference:
Add to this…
Discovery 7: Shakespeare / Dee reveal the latitude/longitude coordinates of the Great Pyramid of Giza.
If a gigantic “DOES NOT COMPUTE” sign is flashing before your eyes you’re not alone. Even today, in the highly connected twin worlds of cryptography and mathematics, there’s nothing to compare this to. We can either accept this revolutionary new information as a challenge, bringing our combined intellects together to explore it and see where it leads. Or we can throw up our hands in resignation and ignore it, hoping it’ll go away.
That’s usually the case with paradigm shifts. We pretend they’re not happening. Until they have.
Book II in The Holy Trinity Series, BARDCODE, takes us even further down the rabbit hole to suggest there’s another way of looking at this, even if we can’t fully understand it all yet.
Albert Einstein often said he solved his most complex problems not through intellect, but through intuition, and that it required remaining open and as receptive as a child. He also believed that for a solution to be true it must, above all, be beautiful.
“The pursuit of truth and beauty is a sphere of activity in which we are permitted to remain children all our lives.”
This astounding conundrum Dee and Shakespeare created presents us with a unique opportunity to embrace Einstein’s statement. For it certainly cannot be grasped by intellect alone.
And I defy anyone to say it’s not beautiful.
“ Not from the stars do I my judgment pluck,
And yet methinks I have Astronomy,
…
But from thine eyes my knowledge I derive,
And, constant stars, in them I read such art
As truth and beauty shall together thrive. ”
— Sonnet 14
Footnote
A few astute observers have commented that they think they’ve spotted an error in the BARDCODE video concerning the 3:4:5 triangle, GEB. The error is not in the mathematics, however, it’s in my omission of slides for that triangle. I had already decided it was too much for a general audience. And I knew it was going to require going into the more complex details you’ve now seen. But in the video, whilst showing the calculations for the Tribonacci constant (T), the Euler-Mascheroni constant (γ), and √3, I used the average hypotenuse, 37.79, without explaining it. Observers then assumed that hypotenuse for the 3:4:5 triangle (instead of its actual value, 37.89) and of course that fails the Pythagorean Theorem test.
This was a serious oversight on my part and I apologize for the confusion it caused. To alert future viewers, I’ve now added an explanatory note in the description field of the BARDCODE video.
Click here to continue to Universal Constant of Measure
